show that the product of two triangular matrices is itself triangular
To show that the product of two triangular matrices is itself triangular, we will consider two types of triangular matrices: upper triangular and lower triangular matrices. For this solution, we will focus on upper triangular matrices.
1. Define Upper Triangular Matrices:
Let A and B be two upper triangular matrices. An upper triangular matrix is defined as a square matrix where all the entries below the main diagonal are zero.
For example:
A=⎛⎜⎝a11a12a130a22a2300a33⎞⎟⎠,B=⎛⎜⎝b11b12b130b22b2300b33⎞⎟⎠
2. Multiply the Matrices:
We will compute the product C=AB where C is defined as:
C=⎛⎜⎝c11c12c13c21c22c23c31c32c33⎞⎟⎠
The entries of C can be calculated as follows:
- c11=a11b11
- c12=a11b12+a12b22
- c13=a11b13+a12b23+a13b33
- c21=0⋅b11+a22b22=a22b22
- c22=0⋅b12+a22b23+0⋅b33=a22b23
- c23=0⋅b13+a23b33=a23b33
- c31=0⋅b11+0⋅b22+a33b33=0
- c32=0⋅b12+0⋅b23+0⋅b33=0
- c33=0⋅b13+0⋅b23+a33b33=a33b33
3. Construct the Result Matrix:
Now, we can construct the resulting matrix C:
C=⎛⎜⎝c11c12c130c22c2300c33⎞⎟⎠
where c11,c12,c13,c22,c23,c33 are all defined above.
4. Conclusion:
Since all the entries below the main diagonal of matrix C are zero, we conclude that the product AB is also an upper triangular matrix.
Let A and B be two upper triangular matrices. An upper triangular matrix is defined as a square matrix where all the entries below the main diagonal are zero.
A=⎛⎜⎝a11a12a130a22a2300a33⎞⎟⎠,B=⎛⎜⎝b11b12b130b22b2300b33⎞⎟⎠
We will compute the product C=AB where C is defined as:
C=⎛⎜⎝c11c12c13c21c22c23c31c32c33⎞⎟⎠
- c11=a11b11
- c12=a11b12+a12b22
- c13=a11b13+a12b23+a13b33
- c21=0⋅b11+a22b22=a22b22
- c22=0⋅b12+a22b23+0⋅b33=a22b23
- c23=0⋅b13+a23b33=a23b33
- c31=0⋅b11+0⋅b22+a33b33=0
- c32=0⋅b12+0⋅b23+0⋅b33=0
- c33=0⋅b13+0⋅b23+a33b33=a33b33
Now, we can construct the resulting matrix C:
C=⎛⎜⎝c11c12c130c22c2300c33⎞⎟⎠
where c11,c12,c13,c22,c23,c33 are all defined above.
Since all the entries below the main diagonal of matrix C are zero, we conclude that the product AB is also an upper triangular matrix.
Topper's Solved these Questions
- MATRICES BOOK - FIITJEECHAPTER - MATRICES EXERCISE - SOLVED PROBLEM
32 Videos
- MATRICES BOOK - FIITJEECHAPTER - MATRICES EXERCISE - ASSIGNMENT PROBLEM (SUBJECTIVE) (Level-I)
12 Videos
- MATRICES BOOK - FIITJEECHAPTER - MATRICES EXERCISE - NUMERICAL BASED
3 Videos
- MATHEMATICS TIPSBOOK - FIITJEECHAPTER - MATHEMATICS TIPSEXERCISE - NUMERICAL DECIMAL BASED QUESTIONS
21 Videos
- PARABOLABOOK - FIITJEECHAPTER - PARABOLAEXERCISE - NUMERICAL BASED
5 Videos
Similar Questions
Knowledge Check
A triangular age pyramid has
Adeclining populationBincreasing populationCstable populationDfluctuating populationWho won the triangular struggle?
ARashtrakutasBChalukyasCof sailsDruler Nagabhata II
Show that the two matrices A,P−1AP have the same characteristic roots
View SolutionFind the volume of the triangular prism shown in the diagram.
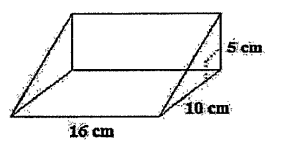
View SolutionNull matrix upper triangular matrix and lower triangular matrix
View SolutionWhich of the following is a triangular matrix? (A) a scalar matrix (B) a lower triangular matrix (C) an upper triangular matrix (D) a diagonal matrix
View SolutionIn a square matrix A=[aij] if i>j and aij=0 then matrix is called
Square matrix
Lower triangular matrix
Upper triangular matrix
Unit matrix
View SolutionName each of the following 3-dimensional shapes.
(i) It has one triangular base and three triangular faces.
(ii) It has two opposite pentagonal bases while other faces are rectangles.
(iii) It has one curved face and two circular plane faces.
View Solution

