क्रमश: 10−8C और −10−8C आवेश वाले दो बिन्दु आवेश q1 और q2, एक दूसरे से 0.1 m दूर रखे हुए हैं। चित्र 2.44 के अनुसार A, B और C बिन्दुओं पर वैद्युत क्षेत्र ज्ञात करें।
बिन्दु A पर वैद्युत क्षेत्र: मान लें बिन्दु A पर परिणामी वैद्युत →Ea क्षेत्र है जहाँ
→Ea=→Ea1+→Ea2
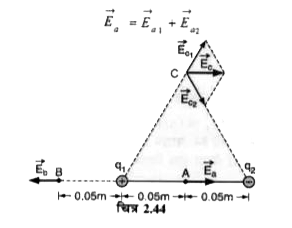
स्पष्ट है कि Ea1 (आवेश q1 का बिन्दु A पर वैद्युत क्षेत्र)
=(9×109Nm2/C2)×10−8C(0.05m)2=3.6×104N/C तथा →Ea2 (आवेश q2 का बिन्दु A पर वैद्युत क्षेत्र) = 3.6×104N/C →Ea1और →Ea2, दोनों एक ही दिशा में हैं अर्थात् दाई ओर, इसलिए →Ea भी दाईं ओर है अर्थात् आवेश q1 से आवेश q2 को ओर। अत: Ea=Ea1+Ea2=7.2×104N/C
बिन्दु । पर वैद्युत क्षेत्रः मान लें बिन्दु B पर परिणामी वैद्युत क्षेत्र →Eb, है, जहाँ
→Eb=→Eb1+→Eb2
स्पष्टत: Eb1 (आवेश q1 का बिन्दु B पर वैद्युत क्षेत्र)
=(9×109Nm2/C2)×10−8(0.05m)2=0.4×104N/C
यह बात ध्यान देने वाली है कि →Eb1 , बाईं ओर है और →Eb2 , दाई ओर। स्पष्ट है कि →Eb की दिशा →Eb1 की ओर है (क्योंकि Eb1>Eb2 )| इस प्रकार
Eb=Eb1−Eb2
=3.6×104N/C−0.4×104N/C
=3.2×104N/C
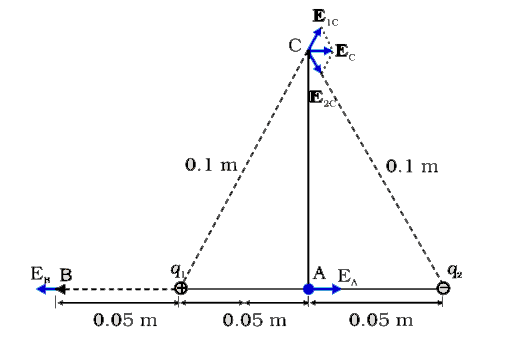
बिन्दु C पर वैद्युत क्षेत्रः मान लें बिन्दु C पर वैद्युत क्षेत्र →Ec है, जहाँ
Ec=Ec1−Ec2
क्योंकि बिन्दु C, आवेशों +q और -q से एक जैसी दूरी पर है, अत:
Ec1=Ec2=(9×109Nm2/C2)10−8C(0.1m)2=9×103N/C
क्योंकि →Ec1 और →Ec2 के बीच का कोण 120° है. इसलिए
Ec=√E2c1+E2c2+2Ec1Ec2cos120∘
=
⎷(9×103)2+(9×103)2+2×(9×103)×(9×103)(−1/2)
या Ec=9×103N/C
→Ec1 और →Ec2 के बीच के कोण को →Ec बराबर बाँटती है, इसलिए यह q1 और q2 को जोड़ने वाली रेखा के समान्तर और बाई से दाई ओर को है।
Similar Questions
Two point charges q1 and q2 of magnitude + 10−8 c and −10−8 c respectively are placed 0.1 m apart calculate the electric fields at points a, b and c

View SolutionTwo point charges q1 and q2 of magnitude + 10−8 c and −10−8 c respectively are placed 0.1 m apart calculate the electric fields at points a, b and c

View SolutionTwo point charges q1andq2, of magnitude +10–8Cand–10–8C, respectively, are placed 0.1 m apart. Calculate the electric fields at points A, B and C shown in Fig. 1.14.
View Solutionगतिमान आवेश और चुंबकत्व पर महत्वपूर्ण प्रश्न
View Solutionवैद्युत आवेश एवं वैद्युत क्षेत्र
View SolutionTwo point charges q_(1) and q_(2) of magnitude + 10^(-8) c and -10^(-8) c respectively are placed 0.1 m apart calculate the electric fields at points a, b and c
View SolutionRecap|एक बिन्दु आवेश के कारण विभव |आवेश के निकाय के कारण वेधयुत विभव |दो बिन्दुओ के बीच विभवांतर |Summary
View Solutionआवेश व उसके प्रकार#!# आवेश के गुणधर्म और उस पर आधारित प्रशन #!# आवेश को उत्पन करने की विधिया
View Solution

