Two charges ±10μC are placed 5.0 mm apart. Determine the electric field at (a) a point P on the axis of the dipole 15 cm away from its centre O on the side of the positive charges, as shown in Fig. (a) and (b) be a point Q, 15 cm away from O on a line passing through O and normal to the axis of the dipole, as shown in Fig (b). 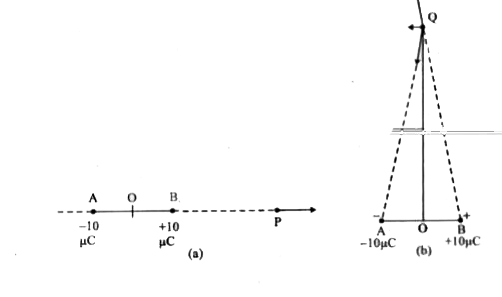 Solution in Tamil
Solution in Tamil
Field at P due to charge +10μC=10−54π(8.854×10−12)×1(15−0.25)2×10−4
=4.13×106NC−1 along BP
Field at P due to charge −10μC=10−54π(8.854×10−12)×1(15+0.25)2×10−4
The resultant electric field P due to the two charges at A and B is =2.7×105NC−1 along BP. In this example, the ratio OP/OB is quite large (= 60). Thus, we can expect to get approximately the same result as above by directly using the formula for electric field at a far-away point on the axis of a dipole.
For a dipole consisting of charges ±q, 2a distance apart, the electric field at a distance r from the centre on the axis of the dipole has a magnitude E=2p4πε0r3 when r>>a
where p=2a q is the magnitude of the dipole moment.
The direction of electric field on the dipole axis is always along the direction of the dipole moment vector (i.e., from -q to q). Here, p=10−5×5×10−3=5×10−8Cm
Therefore E=2×5×10−84π(8.854×10−12)×1(15)2×10−6=2.6×105NC−1
along the dipole moment direction AB, which is close to the result obtained earlier.
Field at Q due to charge +10μC at B =10−54π(8.851×10−12)×1[152+(0.25)2]×10−4
Field at Q due to charge −10μC at A=10−54π(8.854×10−12)×1[152+(0.25)2]×10−4
=3.99×106NC−1 along QA.
Clearly, the components of these two forces with equal magnitudes cancel along the direction OQ but add up along the direction parallel to BA. Therefore, the resultant electric field at due to the two charges at A and B is =2×0.25√152+(0.25)2×3.99×106 along BA=1.33×105NC−1 along BA.
As in (a), we can expect to get approximately the same result using the formula for dipole field at a point on the normal to the axis of the dipole.
When r>>a,E=p4πε0r3=5×10−84π(8.854×10−12)×1(15)3×10−8=1.33×105NC−1
The direction of electric field in this case in opposite to the direction of the dipole moment vector.
Similar Questions
Tow charges pm10 mu C are placed 5.0 mm apart determine the electric field at (a) a point p on the axis of the dipole 15 cm away from its centre o ont the side of the positive charge as (a) and (b) a point q 15 cm away from o on a line passing through o and normal to the axis of the dipole as
View SolutionTwo charges ±10μC are placed 5⋅0mm apart. Determine the electric field at (a) point P on the axis of dipole 15cm away from its center on the side of the positive charge. As shown in Figure and at (b) a point Q. 15cm away form O on a line passing through O and a line passing through O and normal to the axis of the dipole as shown in Fig.
View SolutionTwo charges of dipole +- 10 mu C are placed 1mm apart. Determine the electric field at a point on the axis of the dipole 10 cm away from its centre and at 10 cm away from centre on the equator of the dipole.
View SolutionTow charges ±10μ C are placed 5.0 mm apart determine the electric field at (a) a point p on the axis of the dipole 15 cm away from its centre o ont the side of the positive charge as (a) and (b) a point q 15 cm away from o on a line passing through o and normal to the axis of the dipole as
View SolutionTwo charges +20muC and -20muC are placed 10mm apart. The electric field at point P, on the axis of the dipole 10 cm away from its centre O on the side of the positive charge is
View SolutionTwo charges 10μC are placed 5.0 mm apart. Determine the electric field at a point P on the axis of the dipole 15 cm away from its centre O on the side of the positive charge, as shown in Fig.
View SolutionTwo charges +- 10 muC are placed 5xx10^(-3) m apart. Determine the electric field at a point Q, 0*15m away from O, on a line passing through O and normal to the axis of the dipole.
View SolutionElectric Field Due to an Electric Dipole Two charges ±5μC are placed 5 mm apart. Determine the electric field at
a point X on the axis of dipole 10 cm away from its centre O on the side of the positive charge as shown in Fig. (a).
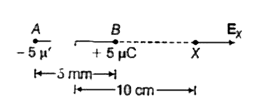
View Solution
