A road roller of 200 kg wt slides on ground when pushed by a lever AB of length 1m, as shown in the figure. The force required to slide the roller acts at a distance of 5cm from the fulcrum. If the coefficient of friction between the roller and the ground is √2 find the effort required to move the roller. (Take g=10ms−2)

The various forces acting on the road roller are shown below in figure.
Let the force required to slide the roller be F. The component of the force F, to overcome the force of friction fs is
Fcosθ=Fcosθ45∘=F√2 (1)
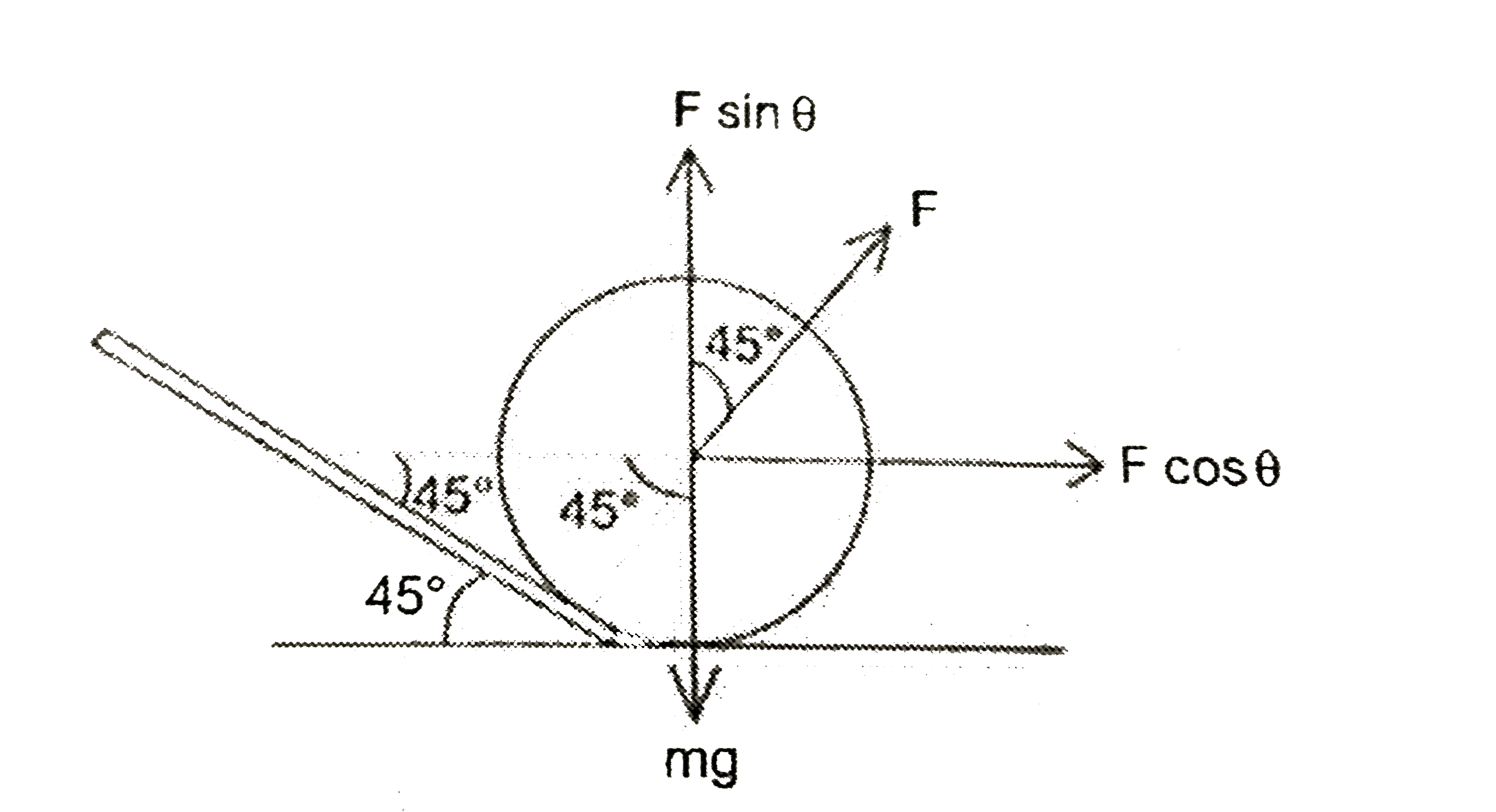
The force of friction fs=μN whereN=mg−Fsinθ
substituting mg =200×10=2000N
sinθ=sin=45∘
N=2000−F√2
The frictional force fs
fs=μN=√2×(200−F√2)
fs=2000√2−F (2)
Equationg (1) and (2)
F√2=2000√2−F
F=4000−√2F
F=4000√2+1=4000√2+1×√2−1√2−1
=4×414=1656N
Applying the law of moments to the lever,
E × effort arm = load × load arm
E×1=1656×0.05
E=82.8N≅83N (approximately)
Similar Questions
A wooden crate with a heavy machine weighing 3000 N slides on the ground when pushed by a lever AB of length 100 cm as shown in the figure. The force required to slide the crate acts at a distance of 10 cm from the fulcrum . If the coefficient of friction between the crate and the ground is √2, find the effort required to move the crate. (Take the value of √2=1.4)

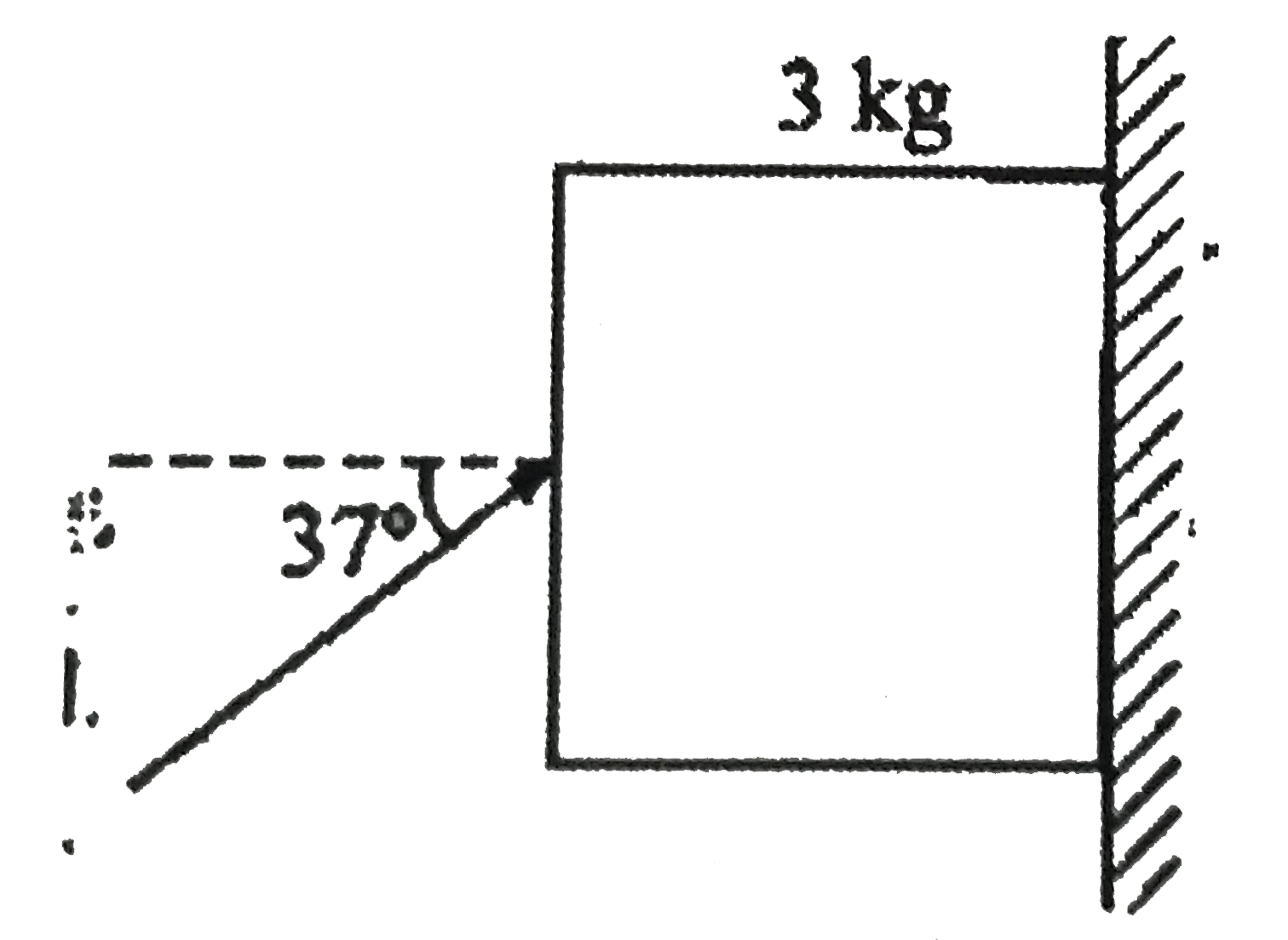
View SolutionA force of 200N is applied as shown in the figure on block of 3 kg. The coefficient of friction between the block and the wall is 0.3. Find the friction acting on the block. (in N) {Take g = 10 m/s2

View Solution
Knowledge Check
A force of 100N is applied on a block of mass 3 kg as shown in the figure-2.164. The coefficient of friction between the surface and the block is 0.25.The frictional force acting on the block is: (Take g=10ms2)
 A15 N downwardsB25 N upwardsC20 N downwardsD30 N upwards
A15 N downwardsB25 N upwardsC20 N downwardsD30 N upwardsA cylinder of 10 kg is sliding in a plane with an initial velocity of 10 m / s . If the coefficient of friction between the surface and cylinder is 0.5 then before stopping, it will cover. (g=10m/s2)
A2.5 mB5 mC7.5 mD10 mA block of mass 50 kg slides over a horizontal distance of 1m. If the coefficient of friction between their surface is 0.2, then work done against friction is (take g=9.8m/s2) :
A98 JB72 JC56 JD34 J
A bullet fired horizontally with a speed of 400m/sec. It strikes a wooden block of mass 5kg initially at rest placed on a horizontal floor as shown in the figure.It emerges with a speed of 200m/sec and the block slides a distance 20cm before coming to rest.Find the coefficient of friction between block and the surface.Mass of bullet is 20g . (take g=10ms2)
View SolutionA block A with mass 100kg is resting on another block B of mass 200kg. As shown in figure a horizontal rope tied to a wall hold it. The coefficient of friction between A and B is 0.2 while coefficient of friction between B and the ground is 0.3 . the minimum required force F to start moving B will be.

View SolutionA block of mass 10 kg is sliding on a surface inclined at 30∘ with horizontal . If coefficient of friction between the block and the surface is 0.5 , find acceleration produced in the block . Take g=9.8m/2 .
View SolutionA block A of mass 100 kg rests on another block B of mass 200 kg and is tied to a wall as shown in the figure. The coefficient of friction between A and B is 0.2 and that between B and ground is 0.3. The minimum force required to move the block B is (g=10ms−2)
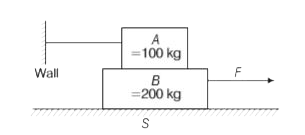
View SolutionA block A with mass 100kg is resting on another block B of mass 200kg. As shown in figure a horizontal rope tied to a wall hold it. The coefficient of friction between A and B is 0.2 while coefficient of friction between B and the ground is 0.3 . the minimum required force F to start moving B will be.

View Solution
