Match the statements/expressions given in Column I with the given in Column II.

Text Solution
The correct Answer is:A→r,B→q,s;C→r,s;D→p,r
(A) Let y=x2+2x+4x+2
⇒x2+(2−y)x+(4−2y)=0
⇒(2−y)2−4(4−2y)≥0 [∵D≥0]
⇒y2+4y−12≥0⇒y≤−6,y≥2
∴ Minimum value of y is 2.
(B) Since, (A+B)(A−B)=(A−B)(A+B)
⇒A2−AB+BA−B2=A2+AB−BA−B2
⇒AB=BAand(AB)t=(−1)kAB
⇒BtAt=(−1)kAB
⇒−B⋅A=(−1)kAB [∵Bt=−B,At=A]
⇒B⋅A=(−1)k+1AB
⇒(−1)k+1=1
∴K+1 is even of k is odd.
(C ) 1<2(−k+3−a)<2⇒0<−k+3−a<1
Given, a=log3log32
⇒3a=log32⇒3−a=log23 ...(i)
∴k<log23<2 ...(ii)
and1+k>log23>1⇒k>0 ...(iii)
From Eqs. (ii) and (iii),
0<k<2
⇒k=1 [since, k is an integer ]
(D) sinθ=cosϕ
⇒cos(π2−θ)=cosϕ
⇒π2−θ=2nπ±ϕ,n∈I
⇒θ±ϕ−π2=−2nπ,n∈I
⇒1n(θ±ϕ−π2)=−2n,n∈I
|
Similar Questions
Knowledge Check
Match items given in Column I with those given in Column II
 AA = t, B= r, C = p, D = sBA = q, B = s, C = r, D = pCA = s, B= r, C = q, D = tDA = r, B = t, C = p, D = q
AA = t, B= r, C = p, D = sBA = q, B = s, C = r, D = pCA = s, B= r, C = q, D = tDA = r, B = t, C = p, D = q
Match the statements/expressions given in Column I with the values given in Column II.

View SolutionMatch the statements/expressions given in Column I with the values given in Column II.

View SolutionMatch the statements/expressions given in Column I with the values given in Column II. '

View SolutionMatch the statement given in Column I with the phenomenon given in Column II.

View SolutionMatch the statement given in Column I with the phenomenon given in Column II.

View SolutionMatch the statement given in Column I. with the phenomenon given in column II.
View SolutionMatch the detergents given in Column I with their uses given in Column II.
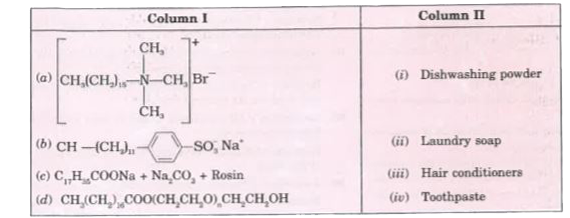
View Solution



