If I1,I2 ,and I3 are moments of inertia of a disc about its geometric axis,diameter and a tangent in its plane,then
Step by step video & image solution for If I_(1),I_(2) ,and I_(3) are moments of inertia of a disc about its geometric axis,diameter and a tangent in its plane,then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Moment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is
A52IB3IC32ID2IThe moment of inertia of a ring about its geometrical axis is I, then its moment of inertia about its diameter will be
A1 IBI/2CIDI/4The moment of inertia of a disc of mass M and radius R about a tangent to its rim in its plane is
A23MR2B32MR2C45MR2D54MR2
Moment of inertia of a disc about an axis passing through its centre and perpendicular to its plane is 12MR2. Determine the moment of inertia of this disc about its diameter and about a tangent perpendicular to its plane.
View SolutionThe Moment of inertia of a disc about an axis passing through its centre and perpendicular to its plane is 1 / 2MR2. Derive the values of moment of inertia of the disc about its diameter and about an axis tangential to the disc lying on its plane ?
View SolutionAssuming he expression for the moment of inertia of a thin disc about its diameter, show that the moment of inertia of the disc about a tangent in its plane is 54MR2
View SolutionThe moment of inertia of a then circular disc about an axis passing through its centre and perpendicular to its plane is I. Then, the moment of inertia of the disc about an axis parallel to its diameter and touching the edge of the rim is
View SolutionThe moment of inertia of thin square plate ABCD of uniform thickness about an axis passing through the center O and perpendicular to the plane of the plate is
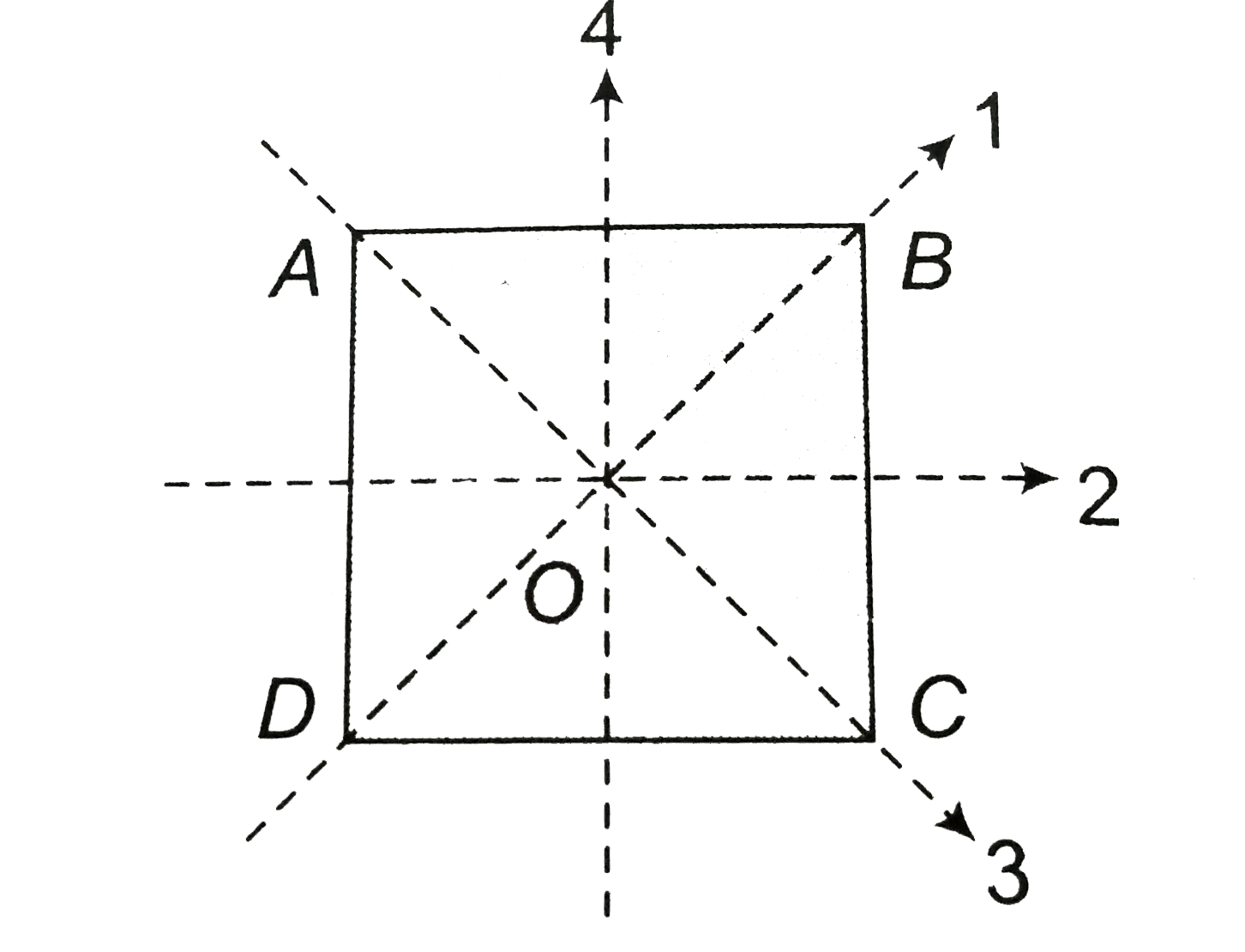
(i) I1+I2
(ii) I2+I4
(iii) I1+I3
(iv) I1+I2+I3+I4
where I1, I2, I3 and I4 are repectively moments of inertia about axes 1, 2, 3 and 4 which are in the plane of the plane
View Solution
