OA, OB, OC are the sides of a rectangular parallelopiped whose diagonals are OO', AA' , BB' and CC' . D is the centre of the rectangle AC'O'B' and D' is the centre of the rectangle O'A'CB' . If the sides OA, OB , OC are in the ratio 1:2:3 , the angle∠DOD' is equal to
cos−1(24)√697
cos−1(22)√619
sin−1(24)√697
sin−1(22)√619
The correct Answer is:A
Topper's Solved these Questions
Similar Questions
If →a=ˆi+ˆj+ˆk,ˆb4ˆi+3ˆj+4ˆkand→c=ˆi+αˆj+βˆk are linearly dependent vectors and |→c|=√3 then (A) α=1,β=−1 (B) α=1,β=±1 (C) α−1,β=±1 (D) α=±1,β=1
View SolutionThe expression 1+sin2αcos(2α−2π)tan(α−3π4)−14sin2α[cotα2+α2)⎤⎥ ⎥⎦ when simplified reduces to
View SolutionOABC is a tetrahedron such that OA=OB=OC=k and each of the edges OA,OB and OC is inclined at an angle theta with the other two the range of theta is
View SolutionThe magnitude of vectors −−→OA,−−→OBand−−→OC in figure are equal. Find the direction of −−→OA+−−→OB−−−→OC.
 .
.
View Solutionदी गई आकृति में OAOC=ODOB है तो सिद्ध कीजिए कि ∠A=∠C तथा ∠B=∠D
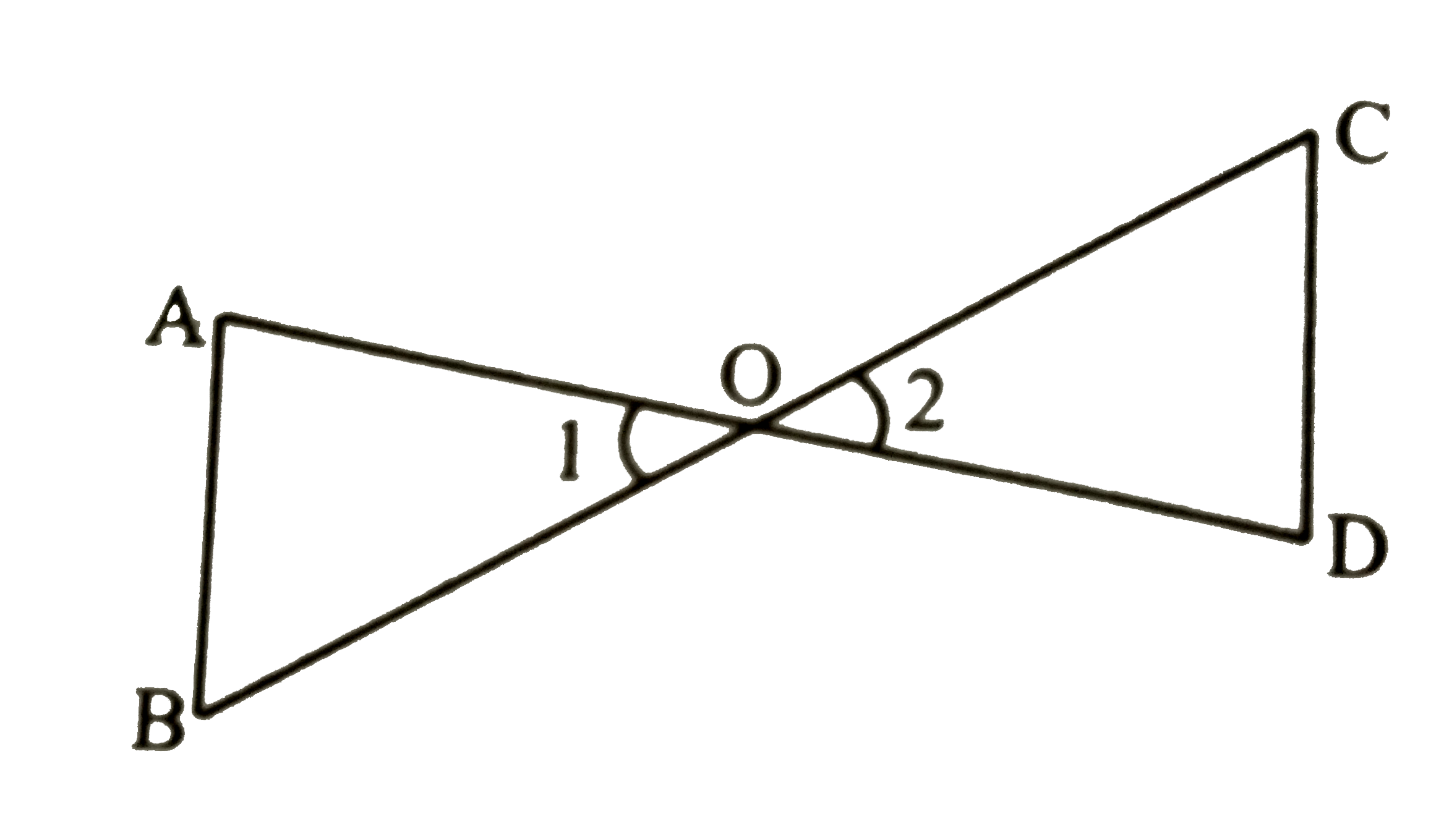
View Solutionचित्र में यदि OA⋅OB=OC⋅OD है तो सिद्ध कीजिए कि ∠A+∠C तथा ∠B=∠D
View Solutionदिखाए गए वेक्टरो −−→OA,−−→OB तथा −−→OC के परिमाण बराबर है। वेक्टर −−→OA+−−→OB−−−→OC की दिशा बताएँ।
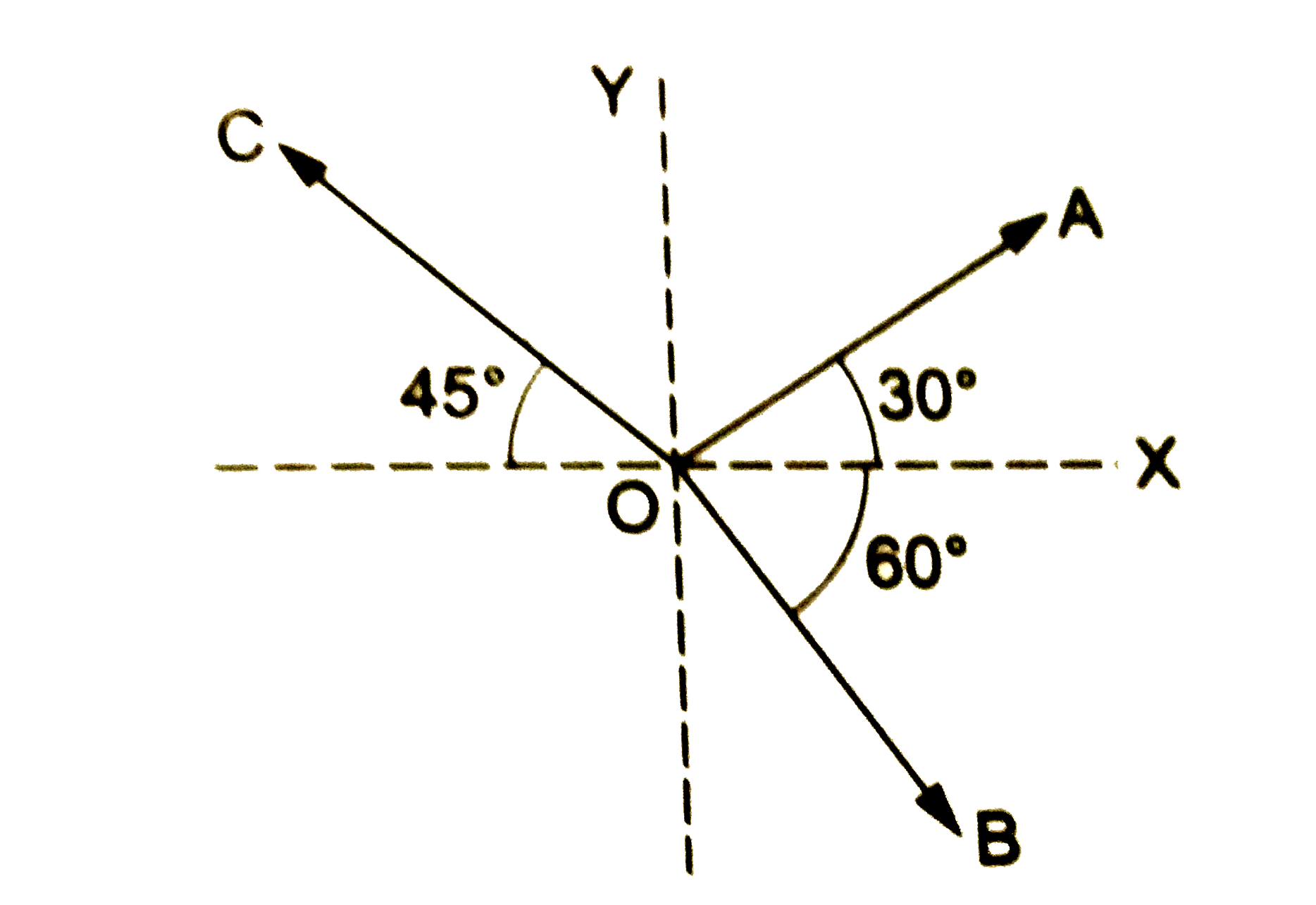
View SolutionIf OA=a, OB=b, OC=c are the co-terminus edges of regular parallelopiped, then the shortest distance between the diagonal and the side OA not meeting the diagonal is
View SolutionIf OA=a, OB=b, OC=c are the co-terminus edges of regular parallelopiped, then the shortest distance between the diagonal and the side OB not meeting the diagonal is
View SolutionIf OAB is a tetrahedron with edges and ˆp,ˆq,ˆr are unit vectors along bisectors of
−−→OA,−−→OB:−−→OB,−−→OC:−−→OC,−−→OA respectively and ˆa=−−→OA∣∣∣−−→OA∣∣∣,→b=−−→OB∣∣∣−−→OB∣∣∣,→c=−−→OC∣∣∣−−→OC∣∣∣, then :
View SolutionIn figure OA. OB= OC. OD
Show that ∠A=∠Cand∠B=∠D
View SolutionIn the figure shown, OABC is a rectangle with OA=3 units, OC = 4 units. If BD = 2.5 units, then the slope of the diagonal OB is equal to
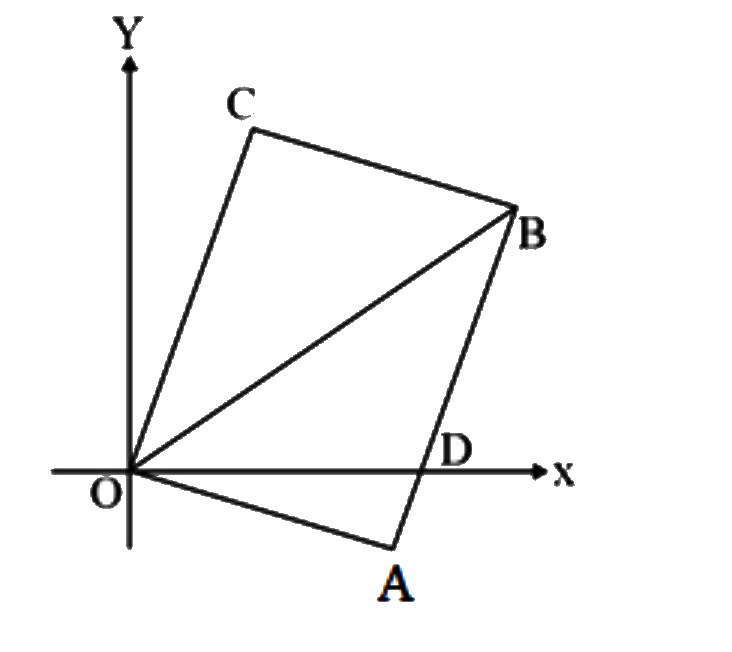
View SolutionIn the side ABCD rectangle (OA + OB) (OA-OB) = _____ cm
View SolutionOAOC=ODOB. Prove that ∠A=∠C and ∠B=∠D.
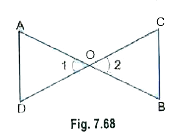
View Solutionवक्तव्य । चित्रानुसार सदिशों OA, OB एवं OC का परिणामी R(1+√2)है। R वृत्त की त्रिज्या है।
वक्तव्य || OA+OC,OB के अनुदिश है तथा (OA+OC)+OB,OB के अनुदिश है।

View Solution

