A 3.0-kg cart moving to the right with a speed of 1.0 m/s has a head-on collision with a 5.0-kg cart that is initially moving to the left with a speed of 2.0 m/s. After the collision, the 3.0-kg cart is moving to the left with a speed of 1.0 m/s. What is the final velocity of the 5.0-kg cart?
zero m/s
0.80 m/s to the right
0.80 m/s to the left
2.0 m/s to the right
The correct Answer is:C
To solve the problem of the collision between the two carts, we will use the principle of conservation of momentum. Here’s a step-by-step solution:
Step 1: Identify the masses and initial velocities
- Mass of cart 1 (m1) = 3.0 kg, initial velocity (u1) = +1.0 m/s (to the right)
- Mass of cart 2 (m2) = 5.0 kg, initial velocity (u2) = -2.0 m/s (to the left)
Step 2: Write down the initial momentum
The total initial momentum (p_initial) of the system can be calculated as:
pinitial=m1⋅u1+m2⋅u2
Substituting the values:
pinitial=(3.0kg⋅1.0m/s)+(5.0kg⋅−2.0m/s)
pinitial=3.0kg m/s−10.0kg m/s=−7.0kg m/s
Step 3: Write down the final momentum
After the collision, the final velocity of cart 1 (v1) is given as -1.0 m/s (moving to the left). Let the final velocity of cart 2 (v2) be V (which we need to find). The total final momentum (p_final) is:
pfinal=m1⋅v1+m2⋅v2
Substituting the known values:
pfinal=(3.0kg⋅−1.0m/s)+(5.0kg⋅V)
pfinal=−3.0kg m/s+5.0kg⋅V
Step 4: Set initial momentum equal to final momentum
According to the conservation of momentum:
pinitial=pfinal
Thus:
−7.0kg m/s=−3.0kg m/s+5.0kg⋅V
Step 5: Solve for V
Rearranging the equation:
−7.0+3.0=5.0⋅V
−4.0=5.0⋅V
V=−4.05.0=−0.8m/s
Conclusion
The final velocity of the 5.0 kg cart is -0.8 m/s, indicating that it is moving to the left.
- Mass of cart 1 (m1) = 3.0 kg, initial velocity (u1) = +1.0 m/s (to the right)
- Mass of cart 2 (m2) = 5.0 kg, initial velocity (u2) = -2.0 m/s (to the left)
The total initial momentum (p_initial) of the system can be calculated as:
pinitial=m1⋅u1+m2⋅u2
Substituting the values:
pinitial=(3.0kg⋅1.0m/s)+(5.0kg⋅−2.0m/s)
pinitial=3.0kg m/s−10.0kg m/s=−7.0kg m/s
After the collision, the final velocity of cart 1 (v1) is given as -1.0 m/s (moving to the left). Let the final velocity of cart 2 (v2) be V (which we need to find). The total final momentum (p_final) is:
pfinal=m1⋅v1+m2⋅v2
Substituting the known values:
pfinal=(3.0kg⋅−1.0m/s)+(5.0kg⋅V)
pfinal=−3.0kg m/s+5.0kg⋅V
According to the conservation of momentum:
pinitial=pfinal
Thus:
−7.0kg m/s=−3.0kg m/s+5.0kg⋅V
Rearranging the equation:
−7.0+3.0=5.0⋅V
−4.0=5.0⋅V
V=−4.05.0=−0.8m/s
The final velocity of the 5.0 kg cart is -0.8 m/s, indicating that it is moving to the left.
Similar Questions
A 0.10-kg cart traveling in the positive x direction at 10.0 m/s collides with a 0.30-kg cart at rest. The collision is elastic. What is the velocity of the 0.10-kg cart after the collision?
View SolutionConsider a man sitting on the cart that is moving with initial and final velocities . Which has 4.54 m/s as the resulting change in speed of the cart?
View SolutionA man of mass 80 kg is riding on a small cart of mass 40 kg which is rolling along a level floor at a speed of 2 m/s. He is runing on the cart so that his velocity relative to the cart is 3 m/s in the direction opposite to the motion of cart. What is the speed of the centre of mass of the system.
View SolutionA man of mass 80 kg is riding on a small cart of mass 40 kg which is rolling along a level floor at a speed of 2 m/s. He is running on the cart so that his velocity relative to the cart is 3 m/s in the direction opposite to the motion of cart. What is the speed of the centre of mass of the system ?
View SolutionA man of mass 80 kg is riding on a small cart of mass 40 kg which is rolling along a level floor at a speed of 2 m/s. He is running on the cart so that his velocity relative to the cart is 3 m/s in the direction opposite to the motion of cart. What is the speed of the centre of mass of the system.
View SolutionA man of mass 80 kg is riding on a small cart of mass 40 kg which is rolling along a level floor at a speed 2 m/s . He is running on the cart , so that his velocity relative to the cart is 3 m/s in the direction opposite to the motion of cart . What is the speed of the centre of the mass of the system ?
View SolutionA cart of mass 0.5kg is placed on a smooth surface and is connected by a string to a block of mass 0.2kg. At the initial moment the cart moves to the left along a horizontal plane at a speed of 7m/s(Use g=9.8m/s2)
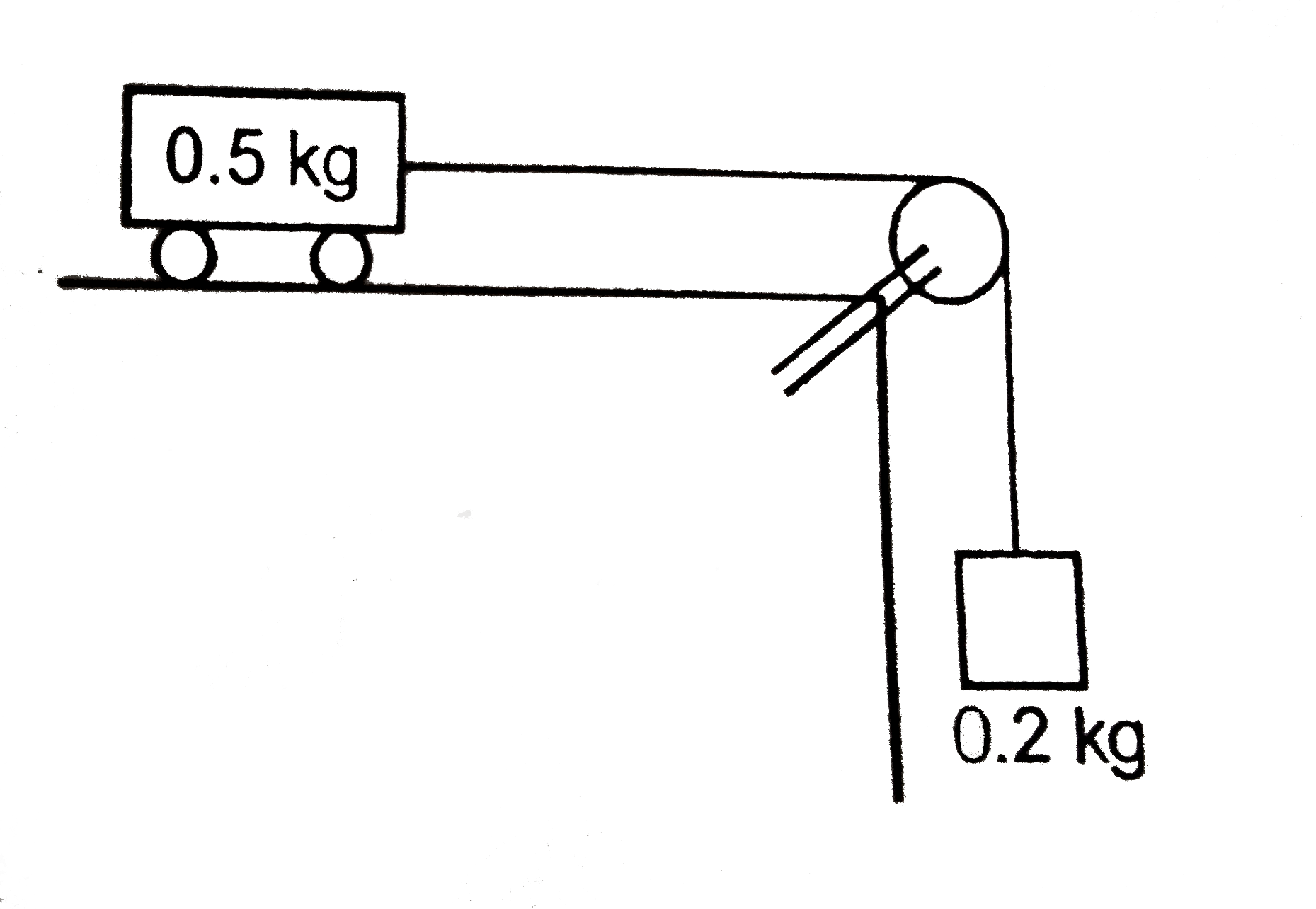
View SolutionA cart is moving horizontally along a straight line with constant speed 30 m/s. A projectile is to be fired from the moving cart in such a way that it will return to the cart after the cart has moved 120m. At what speed (relative to the cart, in m/s) must the projectile be fired ? (Take g=10m//s^2 )
View Solution

