For the damped oscillator of Fig. 15.20, m= 250g, k= 85N/m, and b= 70g/s
How long does it take for the mechanical energy to drop to one-half its initial value?
From Eq. 15.35 the mechanical energy at time t is 1/2kx2me−bt/m
Calculations: The mechanical energy has the value 1/2kx2m at t=0, Thus, we must find the value of t for which
12kx2me−bt/m=12(12kx2m).
If we divide both sides of this equation by 1/2kx2m and solve for t as we did above, we find
t=−mIn12b=−(0.25kg)(In12)0.070kg/s=2.5s.
This is exactly half the time we calculated in (b), or about 7.5 periods of oscillation. Figure 15.21 was drawn to illustrate this sample problem.
Similar Questions
For the damped oscillator of Fig. 15.20, m= 250g, k= 85N/m, and b= 70g/s
How long does it take for the amplitude of the damped oscillations to drop to half its initial value?
View SolutionFor the damped oscillator of Fig. 15.20, m= 250g, k= 85N/m, and b= 70g/s
What is the period of the motion?
View Solution
Knowledge Check
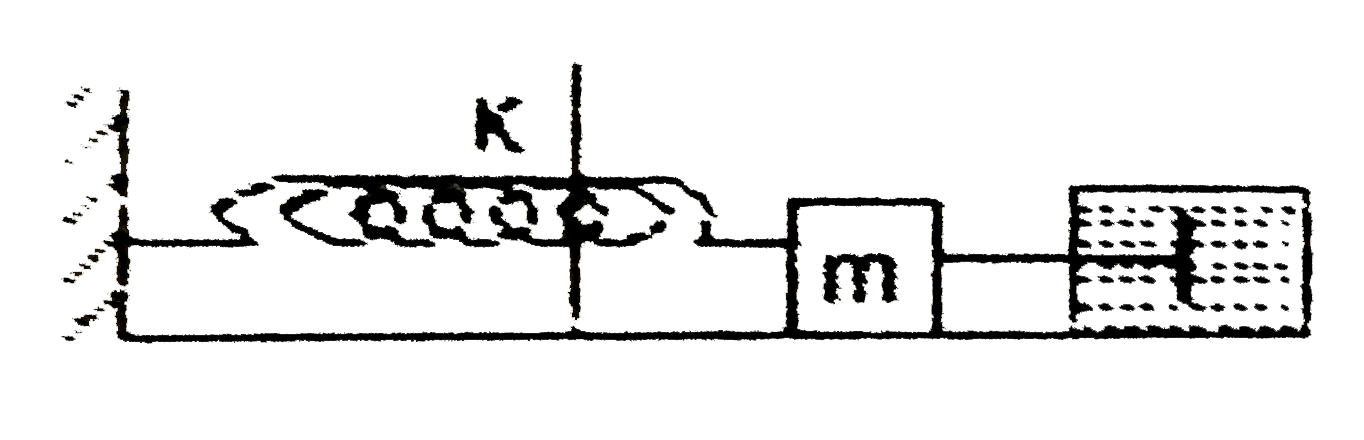
For a damped oscillator which follow the equation →F=−k→x−b→V
the mass of the block is 100 gm K=100N/M and the damping constant is 20 gm/sec. thhen find the time taken for its mechanical energy to drop to one-fourth of its initial value.A1.73B3.46C6.93D13.84The first-order disappearance of a substance has a half-life of 34.0 s. How long does it take for the concentration of that substance to fall to 12.5% of its initial value?
A11 sB68 sC102 sD272 s
Here are three sets of values for the spring constant, damping constant, and mass for the damped oscillator of Fig. 15.17. Rank the sets according to the time required for the mechanical energy to decrease to one-fourth of its initial value, greatest first.
{:(bar("Set 1" 2k_(0)" " b_(0)" " m_(0))),("Set 2 " k_(0) " " 6b_(0) " " 4m_(0)),(ul("Set 3" 3k_(0) " " 3b_(0)" " m_(0))):}
View SolutionFor the damped oscillator shown in previous Figure, the mass m of the block is 400 g, k=45Nm−1 and the damping constant b is 80gs−1. Calculate .
(a) The period of osciallation ,
(b) Time taken for its amplitude of vibrations to drop to half of its initial value and
(c ) The time taken for its mechanical energy to drop to half its initial value.
View SolutionIn damped oscillatory motion a block of mass 20kg is suspended to a spring of force constant 90N/m in a medium and damping constant is 40g/s. Find (a) time period of oscillation (b) time taken for amplitude of oscillation to drop to half of its intial value (c) time taken for its mechanical energy to drop to half of its initial value.
View SolutionFor the damped oscillator shown in Fig, the mass of the block is 200g,k=80Nm−1 and the damping constant b is 40gs−1 Calculate
(a) The period of oscillation
(b) Time taken for its amplitude of vibrations to drop to half of its initial values
(c) The time for the mechanical energy to drop to half initial values
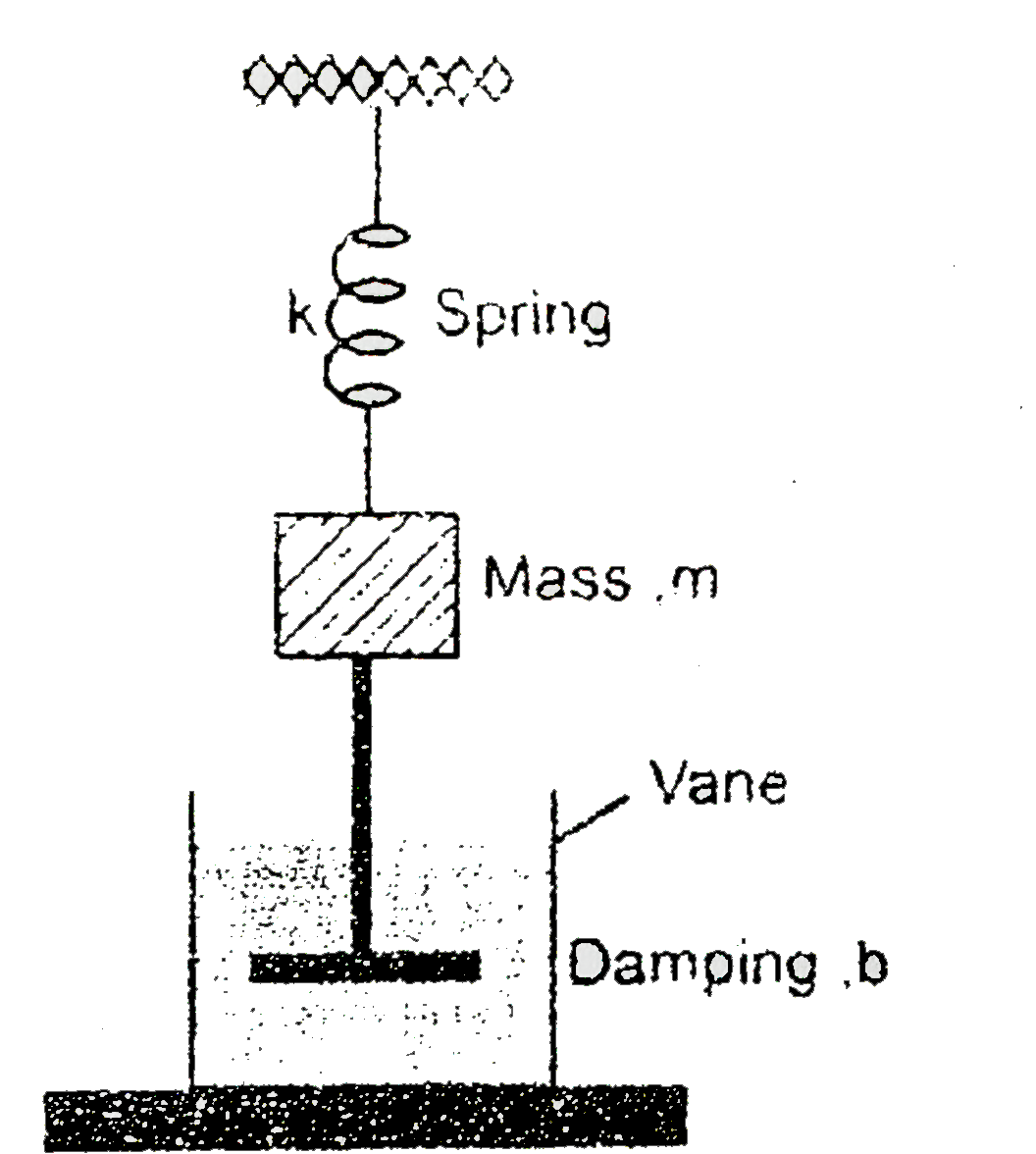
View SolutionAmplitude of mass spring system which is executing SHM decreases with time. If mass = 500g decay constant = 20 g/s then how much time is required for the amplitude of the system to drop to half of its initial value.
View SolutionAmplitude of a mass-spring system, which is executing simple harmonic motion decreases with time. If mass=500g, Decay constant=20 g/s then how much time is required for the amplitude of the system to drop to half of its initial value ? (In 2=0.693)
View Solution

