Write the formula for Inclusion-Exclusion principle and suppose that 100 of 120 mathematics students was college take at least one of the languages French, German and Russian. Also suppose 65 study French 45study German, 42 study Russian, 20 study French and German, 25 study French and Russian 15 study German and Russian. Find the number of student studying all subjects. Also find studying exactly one subject.
Step by step video & image solution for Write the formula for Inclusion-Exclusion principle and suppose that 100 of 120 mathematics students was college take at least one of the languages French, German and Russian. Also suppose 65 study French 45study German, 42 study Russian, 20 study French and German, 25 study French and Russian 15 study German and Russian. Find the number of student studying all subjects. Also find studying exactly one subject. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
In a survey of 200 students of a school, it was found that 120 study Mathematics, 90 study Physics and 70 study Chemistry , 40 study Mathematics and Physics, 30 study Physics and Chemistry, 50 study Chemistry and Mathematics and 20 none of these subjects. Find the number of students who study all the three subjects.
View SolutionIn a survey of xavirs's school of Bhubaneswar of 200 students, It was found that 120 study math, 90 study physics, 70 study shemistry, 40 study math and physics, 30 study physics and chemistry, 50 study chemistry and math and 20 study none of these subjects then the number of students study all the subjects is :
View Solution
Knowledge Check
In a group of 15, 7 have studied German, 8 have studied French and 3 have not studied either . The Venn diagram showing the number of students who have studied both is
A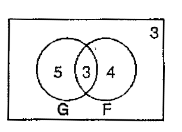 B
B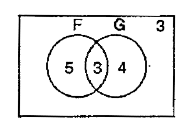 C
C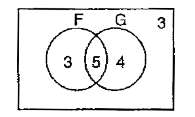 D
D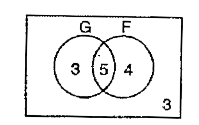
In a survey of 200 students of a school, it was found that 120 study Mathematics, 90 study Physics and 70 study Chemistry , 40 study Mathematics and Physics, 30 study Physics and Chemistry, 50 study Chemistry and Mathematics and 20 none of these subjects. Find the number of students who study all the three subjects.
A30B20C10DNone of TheseIn a class of 70 students, 50 students study HL Mathematics and 25 study SL Physics, if each student studies at least one of the two subjects, then number of students studying only SL Physics, is
A20B15C18D22
Each student in a class of 40, studies at least one of the subjects English, Mathematics and Economics.16 study English, 22 Economics and 26 Mathematics, 5 study English and Economic, 14 Mathematics and Economics and 2 study all the three subjects. The number of students who study English and Mathematics but not Economics is
View SolutionThe given Venn diagram represent the number of students in a class who study three languages, French Spanish and Japanese.
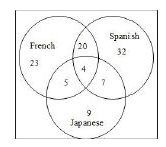
The number of students studying French, Spanish and Japanese is:
View SolutionIn a survey of 200 students of a school, it was found that 120 study Mathematics, 90 study Physics and 70 study Chemistry , 40 study Mathematics and Physics, 30 study Physics and Chemistry, 50 study Chemistry and Mathematics and 20 none of these subjects. Find the number of students who study all the three subjects.
View SolutionIn a University there are 1200 students studying four different subjects, Mathematics, Statistics, Physics and Chemistry. 20% of the total number of students are studying Mathematics, one-fourth of the total number of students are studying Physics, 320 students are studying Statistics and remaining students are studying Chemistry. Three-fifth of the total number of students studying Chemistry are girls. 150 boys are studying Mathematics. 60% of students studying Physics are boys. 250 girls are studying Statistics.
In which subjects is the difference between the number of boys and girls equal ?
View SolutionIn a survey of xavirs's school of Bhubaneswar of 200 students, It was found that 120 study math, 90 study physics, 70 study shemistry, 40 study math and physics, 30 study physics and chemistry, 50 study chemistry and math and 20 study none of these subjects then the number of students study all the subjects is :
View Solution
