If 50.0 cm of copper wire (diameter= 3.00 mm) is formed into a circular loop and placed perpendicular to a uniform magnetic field that is increasing at the constant rate of 30.0 mT/s, at what rate is thermal energy generated in the loop?
To solve the problem step by step, we will follow these steps:
Step 1: Calculate the Area of the Circular Loop
The area A of a circular loop can be calculated using the formula:
A=πr2
where r is the radius of the loop. Given that the diameter D of the wire is 3 mm, the radius r is:
r=D2=3mm2=1.5mm=1.5×10−3m
Now, substituting the radius into the area formula:
A=π(1.5×10−3)2=π(2.25×10−6)≈7.06858×10−6m2
Step 2: Calculate the Resistance of the Wire
The resistance R of the wire can be calculated using the formula:
R=ρLA
where ρ is the resistivity of copper (given as 1.69×10−8Ω⋅m), L is the length of the wire (50 cm = 0.5 m), and A is the area calculated in Step 1.
Substituting the values:
R=1.69×10−8×0.57.06858×10−6≈8.45×10−97.06858×10−6≈1.196×10−3Ω
Step 3: Calculate the EMF Induced in the Loop
The induced EMF E can be calculated using Faraday's law of electromagnetic induction:
E=−dΦdt
where Φ=B⋅A is the magnetic flux.
Given that the magnetic field B is increasing at a rate of dBdt=30.0mT/s=30.0×10−3T/s, we can express the EMF as:
E=A⋅dBdt
Substituting the area and the rate of change of the magnetic field:
E=(7.06858×10−6)⋅(30.0×10−3)≈2.120×10−7V
Step 4: Calculate the Power (Rate of Thermal Energy Generation)
The power P generated in the loop can be calculated using the formula:
P=E2R
Substituting the values of EMF and resistance:
P=(2.120×10−7)21.196×10−3≈4.494×10−141.196×10−3≈3.75×10−11W
Final Answer
The rate at which thermal energy is generated in the loop is approximately:
P≈3.75×10−11W
The area A of a circular loop can be calculated using the formula:
A=πr2
where r is the radius of the loop. Given that the diameter D of the wire is 3 mm, the radius r is:
r=D2=3mm2=1.5mm=1.5×10−3m
Now, substituting the radius into the area formula:
A=π(1.5×10−3)2=π(2.25×10−6)≈7.06858×10−6m2
The resistance R of the wire can be calculated using the formula:
R=ρLA
where ρ is the resistivity of copper (given as 1.69×10−8Ω⋅m), L is the length of the wire (50 cm = 0.5 m), and A is the area calculated in Step 1.
R=1.69×10−8×0.57.06858×10−6≈8.45×10−97.06858×10−6≈1.196×10−3Ω
The induced EMF E can be calculated using Faraday's law of electromagnetic induction:
E=−dΦdt
where Φ=B⋅A is the magnetic flux.
E=A⋅dBdt
Substituting the area and the rate of change of the magnetic field:
E=(7.06858×10−6)⋅(30.0×10−3)≈2.120×10−7V
The power P generated in the loop can be calculated using the formula:
P=E2R
Substituting the values of EMF and resistance:
P=(2.120×10−7)21.196×10−3≈4.494×10−141.196×10−3≈3.75×10−11W
The rate at which thermal energy is generated in the loop is approximately:
P≈3.75×10−11W
Similar Questions
A wire 88 cm long bent into a circular loop is placed perpendicular to the magnetic field of flux density is increased to 3.0 wbm−2. Calculate the value of the emf induced .
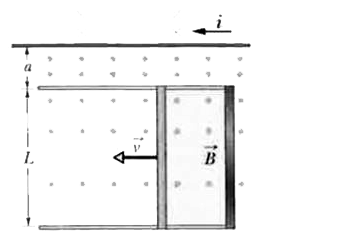
View SolutionFigure 30-50 shows a rod of length L = 12.0 cm that is forced to move at constant speed v = 5.00 m/s along horizontal rails. The rod, rails, and connecting strip at the right form a conducting loop. The rod has resistance 0.400 Ω the rest of the loop has negligible resistance. A current i = 100 A through the long straight wire at distance a= 5.00 mm from the loop sets up a (nonuniform) magnetic field through the loop. Find the (a) emf and (b) current induced in the loop. (c) At what rate is thermal energy generated in the rod? (d) What is the magnitude of the force that must be applied to the rod to make it move at constant speed? (e) At what rate does this force do work on the rod?
View Solution
Knowledge Check
A copper wire of length 50.0 cm and total resistance of 1.1×10−2Ω is formed into a circular loop and placed perpendicular to a uniform magnetic field that is increasing at the constant rate of 10.0 mT/s. At what rate is thermal energy generated in the loop?
A1.32×10−8WB2.36×10−4WC3.62×10−6WD4.23×10−5WRadius of a circular loop placed in a perpendicular uniform magnetic field is increasing at a constant rate of roms−1 If at any instant radius of the loop is r, then emf induced in the loop at that instant will be
A−2Brr0B−2BπrC−Bπrr0D−2Bπrr0Radius ol a circular luop placed in a perpendicular uniform magnetic field is increasing at a constant rate of roms1. If at any instant radius of the loop is r, then emf induced in the loop at that instant will be
A−2brr0B−2BπrC−Bπr0rD−2Bπr0r
A certain elastic conducting material is stretched into a circular loop of 12.0 cm radius. It is placed with its plane perpendicular to a uniform 0.800 T magnetic field. When released, the radius of the loop starts to shrink at an instantaneous rate of 75.0 emfs. What emf is induced in the loop at that instant?
View SolutionA conducting circular loop is placed in a magnetic field of strength 0.04 T, such that the plane of the loop is perpendicular to the magnetic field. If the radius of the loop begins to shrink at a constant rate of 0.5mm/s, then calculate the emf induced in the loop when its radius is 1.5 cm.
View SolutionA circular loop is kept perpendicular to a uniform magnetic field. Loop is rotated about its diameter with constant angular velocity.
View SolutionA circular copper loop is placed perpendicular to a uniform magnetic field of 0.50 T. Due to external forces, the area of the loop decreases at a rate of 1.26×10−3m2/s. Determine the induced emf in the loop.
View SolutionA circular loop of metal wire of radius r is placed perpendicular to uniform magnetic field B. Half of the loop is folded about the diameter with constant angular velocity ω. If resistance of the loop is R then current in the loop is
View Solution
