The displacement of a particle is moving by x=(t−2)2 where x is in metres and t in second. The distance covered by the particle in first 4 seconds is.
4m
8m
12 m
16m
The correct Answer is:b
Given , Displacement , x=(t−2)2
Velocity , v=dxdt=2(t−2)ms−1
Acceleration , a=dvdt=2ms−2
At t=0,v=−4ms−1
At t=2,v=0
At t=4,v=4ms−1
Velocity - time graph is as shown in the figure.
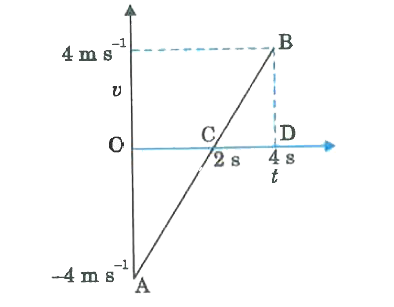
Distance travelled = Area AOC + Area BCD
=12(4×2)+12(4×2)
=8m
The correct option is (b).
Similar Questions
The position x of a particle varies with time t as x=6+12t−2t2 where x is in metre and t is in seconds. The distance travelled by the particle in first five seconds is
View SolutionThe displacement of a particle is given by x = (t-2)^(2) where x is in metre and t in second. The distance covered by the particle in first 4 seconds is
View SolutionThe displacement of a particle is given by x=(t−2)2 where x is in metres and t in seconds. The distance covered by the particle in first 4 seconds is
View SolutionThe displacement of a particle is given by x=(t−2)2 where x is in metres and t in seconds. The distance covered by the particle in first 4 seconds is
View SolutionThe displacement of a particle is moving by x = (t - 2)^2 where x is in metres and t in second. The distance covered by the particle in first 4 seconds is.
View SolutionA particle moves along x-axis obeying the equation x=t(t-1)(t-2), where x (in metres) is the position of the particle at any time t (in seconds). The displacement when the velocity of the particle is zero, is
View SolutionThe displacement x of a particle moving in one dimension under the action of a constant force is related to the time t by the equation t=√x+3, where x is in metre and t is in second. The work done by the force in the first 6 second is
View SolutionThe position of a particle is given by
x=2(t−t2)
where t is expressed in seconds and x is in metre.
The acceleration of the particle is
View Solution

