Determine the intervals of concavity of the curve f(x)=(x−1)3(x−5),x∈R and , points of inflection if any Solution in Tamil
The correct Answer is:x=1,x=3
Step by step video, text & image solution for Determine the intervals of concavity of the curve f(x)=(x-1)^(3)(x-5),x in R and , points of inflection if any by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Determine the intervals of concavity of the curve y=3+sinx.
View SolutionFind the coordinates of the point of inflection of the curve f(x) =e^(-x^(2))
View SolutionFind the intervals in which the graphs of the following functions are concave or convex and locate the points of inflection :
y=x1+x2
View SolutionFind the intervals in which the graphs of the following functions are concave or convex and locate the points of inflection :
y=x+x2/3
View SolutionFind the intervals in which the graphs of the following functions are concave or convex and locate the points of inflection :
y=2−∣∣x5−1∣∣
View SolutionIf f11(x)<0(>0) on an interval (a,b) then the curve y=f(x) on this interval is convex (concave) i.e it is below (above) any of its tangent lines If f11(x0)=0 or does not exist and the second derivative changes sign when passing through the point x0 then the point (x0,f(x)) is the = point of inflection of the curve y=f(x)
If y=x4+x3−18x2+24x−12 then
View SolutionIf f11(x)<0(>0) on an interval (a,b) then the curve y=f(x) on this interval is convex (concave) i.e it is below (above) any of its tangent lines If f11(x0)=0 or does not exist and the second derivative changes sign when passing through the point x0 then the point (x0,f(x)) is the = point of inflection of the curve y=f(x)
y=x4+ax3+32x2+1 is concave along the entire number scale then
View SolutionConcavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
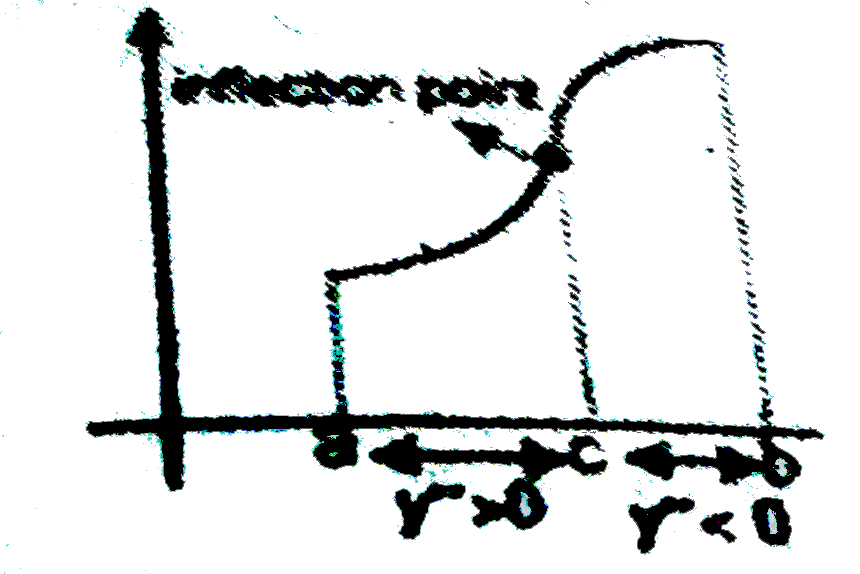
Number of point of inflection for f(x)=(x−1)3(x−2)2 is :
View Solution
