Find the mean deviation about the median for the data given below.
45,36,50,60,53,46,51,48,72,42.
To find the mean deviation about the median for the given data set, we will follow these steps:
Step 1: Arrange the data in ascending order
The given data is:
45,36,50,60,53,46,51,48,72,42.
Arranging this data in ascending order gives us:
36,42,45,46,48,50,51,53,60,72.
Step 2: Find the median
Since there are 10 observations (n = 10), the median is calculated using the formula:
\(
\text{Median} = \frac{\text{n/2 th term} + \text{(n/2 + 1) th term}}{2}
\)
Here, n/2 = 5, so we need to find the 5th and 6th terms.
The 5th term is 48 and the 6th term is 50. Therefore:
\(
\text{Median} = \frac{48 + 50}{2} = \frac{98}{2} = 49.
\)
Step 3: Calculate the deviations from the median
Now we will calculate the absolute deviations of each observation from the median (49):
- |36 - 49| = 13
- |42 - 49| = 7
- |45 - 49| = 4
- |46 - 49| = 3
- |48 - 49| = 1
- |50 - 49| = 1
- |51 - 49| = 2
- |53 - 49| = 4
- |60 - 49| = 11
- |72 - 49| = 23
Step 4: Sum the absolute deviations
Now, we sum all the absolute deviations:
\(
13 + 7 + 4 + 3 + 1 + 1 + 2 + 4 + 11 + 23 = 69.
\)
Step 5: Calculate the mean deviation
Finally, we calculate the mean deviation by dividing the total absolute deviation by the number of observations:
\(
\text{Mean Deviation} = \frac{\text{Total Absolute Deviation}}{\text{Number of Observations}} = \frac{69}{10} = 6.9.
\)
Final Answer
The mean deviation about the median for the given data is 6.9.
---
The given data is:
45,36,50,60,53,46,51,48,72,42.
36,42,45,46,48,50,51,53,60,72.
Since there are 10 observations (n = 10), the median is calculated using the formula:
\(
\text{Median} = \frac{\text{n/2 th term} + \text{(n/2 + 1) th term}}{2}
\)
Here, n/2 = 5, so we need to find the 5th and 6th terms.
\(
\text{Median} = \frac{48 + 50}{2} = \frac{98}{2} = 49.
\)
Now we will calculate the absolute deviations of each observation from the median (49):
- |36 - 49| = 13
- |42 - 49| = 7
- |45 - 49| = 4
- |46 - 49| = 3
- |48 - 49| = 1
- |50 - 49| = 1
- |51 - 49| = 2
- |53 - 49| = 4
- |60 - 49| = 11
- |72 - 49| = 23
Now, we sum all the absolute deviations:
\(
13 + 7 + 4 + 3 + 1 + 1 + 2 + 4 + 11 + 23 = 69.
\)
Finally, we calculate the mean deviation by dividing the total absolute deviation by the number of observations:
\(
\text{Mean Deviation} = \frac{\text{Total Absolute Deviation}}{\text{Number of Observations}} = \frac{69}{10} = 6.9.
\)
The mean deviation about the median for the given data is 6.9.
Similar Questions
Knowledge Check
Find the mean deviation about the median for the data given below :
11, 3, 8, 7, 5, 14, 10, 2, 9A4B5C3D6
Find the mean deviation about the mean for the data in Question:

View SolutionFind the mean deviation about the mean for the data in Question:

View SolutionFind the mean deviation about the mean for the data is Question:

View SolutionFind the mean deviation about the mean for the data is Question:

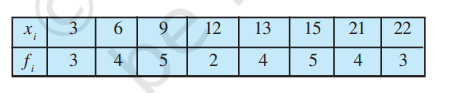
View SolutionFind the mean deviation about the median for the following data:
View SolutionFind the mean deviation about the mean for the following data :

View SolutionFind the mean deviation about the mean for the following data :

View Solution