Three deminsions. Three point particles are fixed in place in a xyz coordinate system. Particle A, at the origin, has mass mA. Particle B, at xyz coordinates (2.00d,1.00d. 200), has mass 2.00mA, and particle C, at coordinates (-1.00d,2.00d,-3.00d), has mass 3.00mA. A fourth particle D,with mass 4.00mA,is to be placed near the other particles. In terms of distance d, at what (a)x, (b)y, and (c)z coordinate should D be placed so that the net gravitational force on A from B, C, and D is zero ?
(a)−1.88d,(b)−3.90d,(c)0.489d. In this way, we are able to deduce that (x,y,z) = (1.88d,3.90d, 0.489d).
Similar Questions
What must be the momentum of a particle with mass m so that the total energy of the particle is 4.00 times its rest energy?
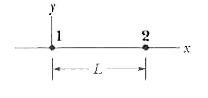
View SolutionIn Fig. 22-19, particle 1 of charge q1=5.00q and a particle 2 of charge q2+2.00q are fixed on the x-axis.
As a multiple of distance L, at what coordinate on the axis is the net electric field of the particles zero?

View Solution
Knowledge Check
The point equidistant from the O(0,0,0),A(a,0,0),B(0,b,0) and C(0,0,c) has the coordinates
A(a,b,c)B(a/2,b/2,c/2)C(a/3,b/3,c/3)D(a/4,b/4,c/4)Three identical point mass each of mass 1kg lie in the x-y plane at point (0,0), (0,0.2m) and (0.2m, 0). The net gravitational force on the mass at the origin is
A1.67×10−9(ˆi+ˆj)NB3.34×10−10(ˆi+ˆj)NC1.67×10−9(ˆi−ˆj)ND3.34×10−10(ˆi+ˆj)NA very large number of particle of same mass m are kept at horizontal distance of 1m,2m,4m,8m and so on from (0,0) point. The total gravitational at this point (0,0) is .
A−8GB−3GmC−4GmD−2Gm
In Fig., particle 1 of charge +q and particle 2 of charge +9.00 q are held at separation L = 8.00 cm on an x axis. If particle 3 of charge q3 is to be located such that the three particles remain in place when released, what must be the (a) x and (b) y coordinates of particle 3, and (c ) the ratio q3/q ?
View SolutionA force (2.00ˆi−4.00ˆj+2.00ˆk)N acts on a particle located at (3.00ˆi+2.00ˆj−4.00ˆk)m. What is the magnitude of the torque on the particle as measured about the origin?
View SolutionThe coordinates of centre of mass of three particles of masses 1 kg, 2 kg, 3 kg are (2m, 2m, 2m). Where should a fourth particle of mass 4 kg be placed so that the coordinates of centre of mass are (4m, 4m, 4m)?
View SolutionThe coordinates of the centre of mass of a system of three particles of mass 1g,2g and 3g are (2,2,2). Where should a fourth particle of mass 4 g be positioned so that the centre of mass of the four particle system is at the origin of the three-dimensional coordinate system ?
View SolutionConsider a system of two particles having masses m1 and m2. If the particle of mass m1 is pushed towards the centre of mass of particles through a distance d, by what distance would the particle of mass m2 move so as to keep the mass centre of particles at the original position?
View Solution

