In the Fig. AD and BE are medians of ΔABCandBE||DF. Prove that CF=(1)(4)AC.Solution in Kannada
Step by step video & image solution for In the Fig. AD and BE are medians of DeltaABC and BE"||"DF. Prove that CF=(1)(4)AC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALSBook:NCERT KANNADChapter:QUADRILATERALSExercise:THINK, DISCUSS AND WRITE
Explore 2 Videos
- QUADRILATERALSBook:NCERT KANNADChapter:QUADRILATERALSExercise:TRY THIS
Explore 1 Video
- PROOFS IN MATHEMATICSBook:NCERT KANNADChapter:PROOFS IN MATHEMATICSExercise:EXERCISE - 15.4
Explore 15 Videos
- REAL NUMBERSBook:NCERT KANNADChapter:REAL NUMBERSExercise:EXERCISE - 1.4
Explore 37 Videos
Similar Questions
Show that the diagonals of a square are equal and bisect each other at right angles.
View SolutionExtend AB to E . Find ∠CBE. What do you notice. What kind of angles are ∠ABCand∠CBE ?
View SolutionState which of the following are mathematical statements and which are not? Give reason.
She has blue rays
View SolutionSimplify the following expressions.
(5+√7)(2+√5)
View SolutionAD BE and CF are the medians of a Delta ABC .Prove that 2(AD+BE+CF)<3(AB+BC+CA)<4(AD+BE+CF)
View SolutionIn Figure, AD, and BE are medians of ABC and BE∣∣DF. Prove that CF=14AC.
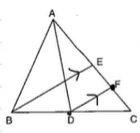
View Solutionदिये गय चित्र में ΔABC की माध्यिकाएं AD और BE हैं। यदि BE∣∣DF तो सिद्ध कीजिए कि CF=14AC.

View Solutionचित्र (13.60) में AD व BE त्रिभुज ABC की माधिकाएँ है तथा BE∣∣DF सिद्ध कीजिए की CF=14AC
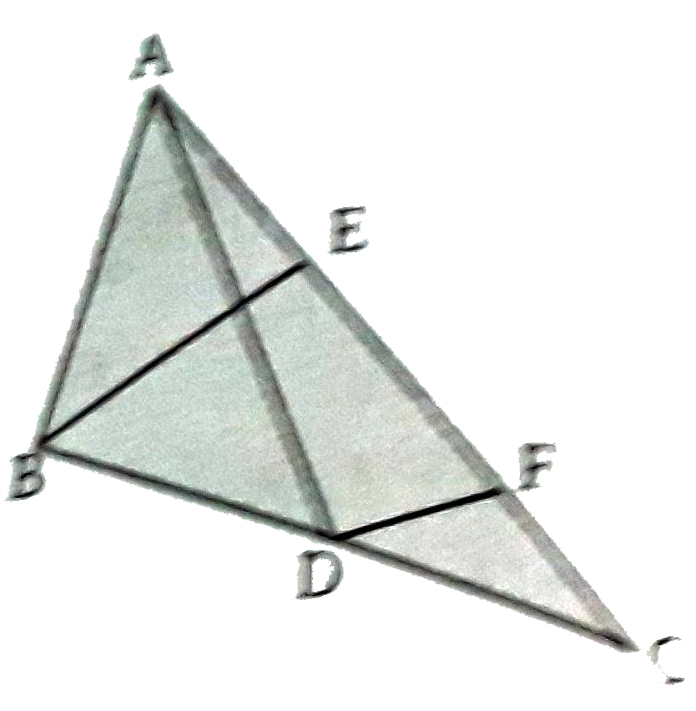
View SolutionIf AD , BE and CF are medians of ΔABC, then ¯¯¯¯¯¯AD+¯¯¯¯¯¯BE+¯¯¯¯¯¯CF =
View SolutionIn the given figure AD and BE are the medians of ΔABC and BE || DF . Prove that CF=1/4AC.
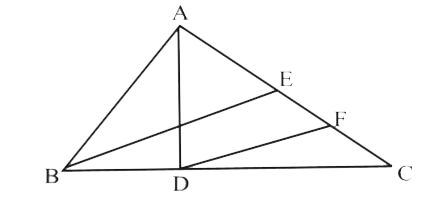
View SolutionIn the Fig. AD and BE are medians of ΔABCandBE||DF. Prove that CF=(1)(4)AC.
View SolutionAD and BE are medians of ΔABC.F'liesonCEandBE||DF. Prove that CF=(14)AC.
View SolutionIn the Fig. AD and BE are medians of ΔABCandBE||DF. Prove that CF=14AC.
View SolutionIn △ABC, AD, BE, CF are the medians. Prove that, 4(AD2+BE2+CF2)=3(AB2+BC2+AC2).
View SolutionDeltaABC In, the median AD, BE and CF intersect at G, then prove that 4(AD+BE+CF)gt3(AB+BC+CA)
View Solution