The relationship between equilibrium constants KpandKc for a gaseous reaction is:
Kc=Kp(RT)Δn
Kp=Kc(RT)Δn
Kp=(KcRT)Δn
Kp=Kc=(RT)Δn
The correct Answer is:B
Step by step video, text & image solution for The relationship between equilibrium constants K_(p) "and" K_(c) for a gaseous reaction is: by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHEMICAL EQULIBRIUMBook:ERRORLESS Chapter:CHEMICAL EQULIBRIUMExercise:JS JEE SECTION (ONLY ONE CHOICE ANSWER (More than one choice correct answer))
Explore 19 Videos
- CHEMICAL EQULIBRIUMBook:ERRORLESS Chapter:CHEMICAL EQULIBRIUMExercise:JS JEE SECTION (ONLY ONE CHOICE ANSWER (Reasoning type question ))
Explore 3 Videos
- CHEMICAL EQULIBRIUMBook:ERRORLESS Chapter:CHEMICAL EQULIBRIUMExercise:CRITICAL THINKING (OBJECTIVE QUESTIONS)
Explore 10 Videos
- CHEMICAL BONDING Book:ERRORLESS Chapter:CHEMICAL BONDING Exercise:JEE Section (Jee (advanced ) 2018)
Explore 1 Video
- CHEMICAL KINETICS Book:ERRORLESS Chapter:CHEMICAL KINETICS Exercise:JEE (Advanced ) 2018
Explore 1 Video
Similar Questions
Knowledge Check
The relationship between equilibrium constants KpandKc for a gaseous reaction is:
AKc=Kp(RT)ΔnBKp=Kc(RT)ΔnCKp=(KcRT)ΔnDKp=Kc=(RT)Δn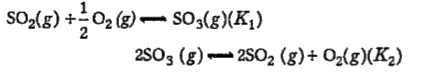
The correct relationship between equilibrium constantsK1 and K2 isAK1=1K2BK1=1√K2CK1=K2Dnone of theseThe unit of equilibrium constant (Kc) in general is
A(mol/lit)B(lit/mol)C(mol/lit)△nD(lit/mol)△n
Determine the values of equilibrium constant (KC)andΔGo for the following reaction :
View SolutionFor a gaseous reaction 2B→A,the equilibrium constant Kp is ……to/than Kc
View SolutionIn a reaction A+B⇔C+D the rate constant of forward reaction & backward reaction is K1 and K2 then the equilibrium constant (K) for reaction is expressed as:
View SolutionThe unit of equilibrium constant Kc for the reaction A+B⇔C would be
View SolutionThe equilibrium constant Kp for a homogeneous gaseous reaction is 10−8. The standard Gibbs free energy change ΔGɵ for the reaction (usingR=2calK−1mol−1) is
View Solution
