Mass of B is four times that of A.B moves with a velocity half that of A. Then, B has
kinetic energy equal to that of A
half the kinetic energy of A
twice the kinetic energy of A
kinetic energy one-fourth of A
The correct Answer is:A
To solve the problem, we need to calculate the kinetic energies of both masses A and B and compare them.
1. Define the Masses and Velocities:
- Let the mass of A be m.
- According to the problem, the mass of B is four times that of A:
Mass of B=4m
- Let the velocity of A be v.
- The velocity of B is half that of A:
Velocity of B=v2
2. Calculate the Kinetic Energy of A:
- The formula for kinetic energy (KE) is given by:
KE=12mv2
- For mass A, substituting the values:
KEA=12mv2
3. Calculate the Kinetic Energy of B:
- Using the same formula for kinetic energy, for mass B we have:
KEB=12(4m)(v2)2
- Simplifying this expression:
KEB=12(4m)(v24)=4mv28=mv22
4. Compare the Kinetic Energies:
- From the calculations, we have:
KEA=12mv2
KEB=12mv2
- Therefore, we can conclude:
KEB=KEA
5. Final Answer:
- B has kinetic energy equal to that of A.
- Let the mass of A be m.
- According to the problem, the mass of B is four times that of A:
Mass of B=4m
- Let the velocity of A be v.
- The velocity of B is half that of A:
Velocity of B=v2
- The formula for kinetic energy (KE) is given by:
KE=12mv2
- For mass A, substituting the values:
KEA=12mv2
- Using the same formula for kinetic energy, for mass B we have:
KEB=12(4m)(v2)2
- Simplifying this expression:
KEB=12(4m)(v24)=4mv28=mv22
- From the calculations, we have:
KEA=12mv2
KEB=12mv2
- Therefore, we can conclude:
KEB=KEA
- B has kinetic energy equal to that of A.
Similar Questions
Two bulbs A and B of equal capacity are filled with He and SO2, respectively, at the same temperature.
(a) If the pressures in the two bulbs are same, what will be the ratio of the velocities of the molecules of the two gases?
(b)At what temperature will the velocity of SO2 molecules become half of the velocity of He molecules at 27∘C?
(c) How will the velocities be affected if the volume of B becomes four times that of A?
(d) How will the velocities be affected if half of the molecules of SO2 are removed from B?
View SolutionThe uncertainties in the velocities of two particles, A and B are 0.05 and 0.02 ms−1, respectively. The mass of B is five times to that of the mass A. What is the ratio of uncertainties (ΔXAΔXB) in their positions
View Solution
Knowledge Check
The two paricles A and B have de Broglie wavelengths 1 nm and 5 nm respectively if mass of A is four times the mass of B, the ratio of kinetic energies of A and B would be :-
A5:1B25:4C20:1D5:4The vapour density of gas A is four times that of B. If moelcular mass of B is M, then molecular mass of A is
AMB4 MCM4D2 MA particle A moving with a certain velocity has a de Broglie wavelength of 1 A. If particle B has mass 25% of that A and velocity 75% of that of A, the de Broglie wavelength of B will be approximately
A1ÅB5.3ÅC3ÅD0.2Å
The density of a gas a is twice that of gas B. Molecular mass of A is half of the molecular of B. The ratio of the partial pressures of A and B is :
View SolutionA particle of mass m moves in the XY plane with a velocity v along the straight line AB. If the angular momentum of the particle with respect to origin O is LA when it is at A and LB when it is at B, then
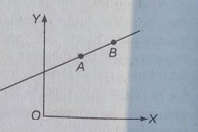
View SolutionA particle of mass m moves in the XY plane with a velocity v along the straight line AB. If the angular momentum of the particle with respect to origin O is LA when it is at A and LB when it is at B, then

View SolutionA particle of mass m moves in the XY plane with a velocity v along the straight line AB. If the angular momentum of the particle with respect to origin O is LA when it is at A and LB when it is at B, then
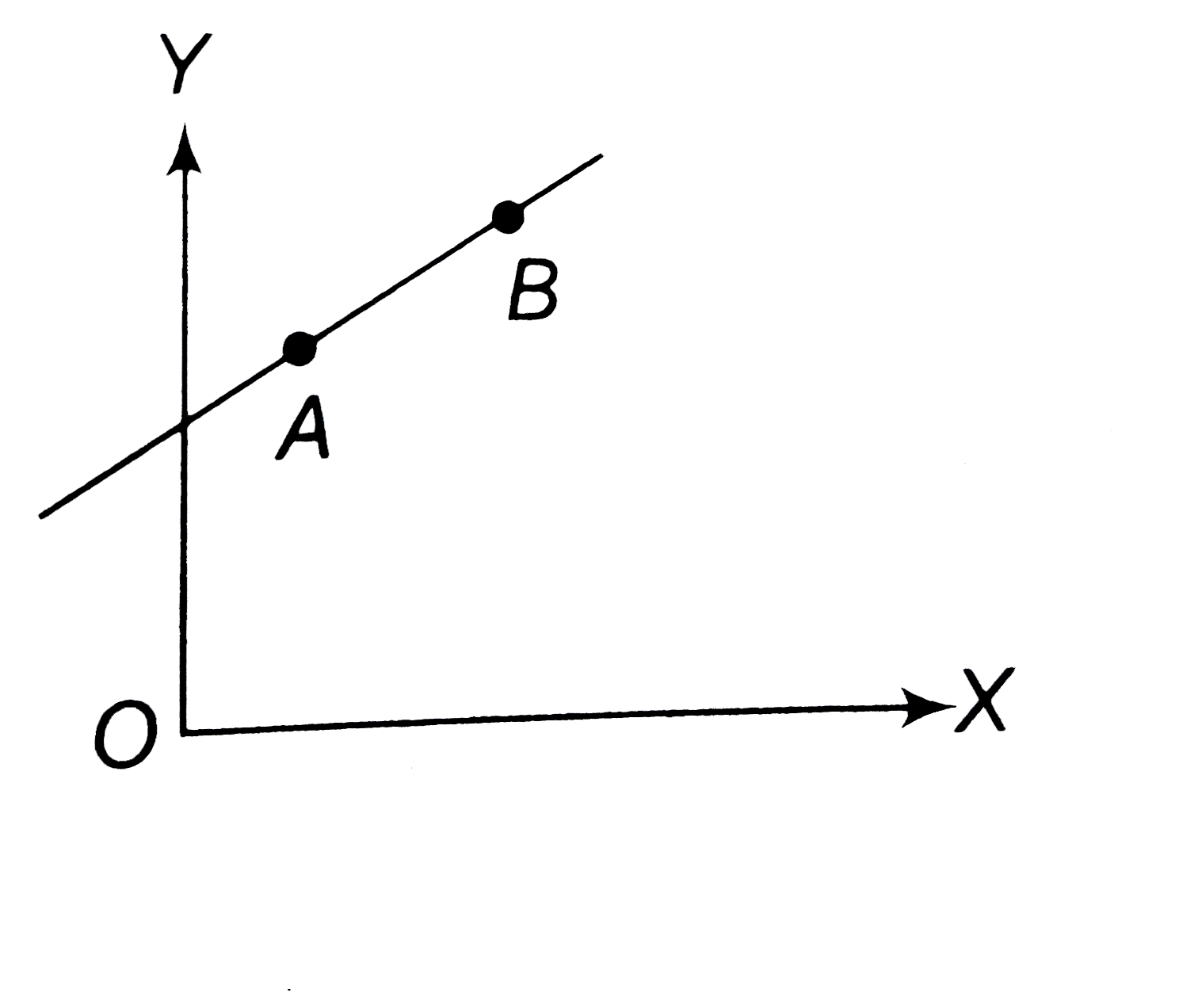
View SolutionThe uncertainties in the velocities of two particles, A and B are 0.05 and 0.02 ms−1, respectively. The mass of B is five times to that of the mass A. What is the ratio of uncertainties (ΔXAΔXB) in their positions
View Solution
