आकृति 6 . 53 में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा AC⊥BD है । दर्शाइए कि
(i) AB2=BC>BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
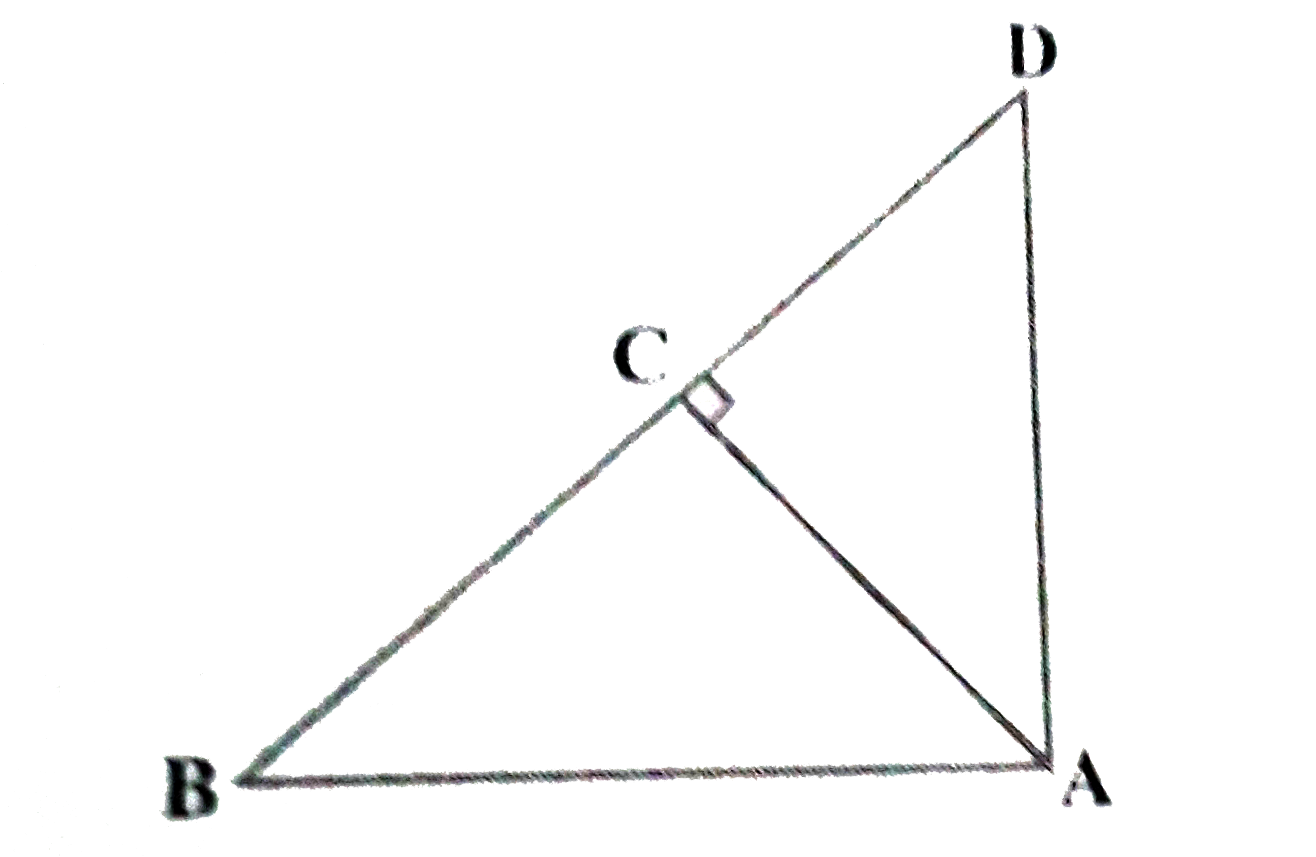
Step by step video & image solution for आकृति 6 . 53 में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा AC bot BD है । दर्शाइए कि (i) AB^(2) = BC gt BD (ii) AC^(2) = BC . DC (iii) AD^(2) = BD . CD by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023समान प्रश्न
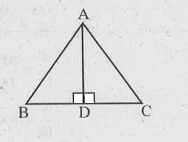
In a △ABC, AB = AC and AD⊥BC, then BD = .......
View SolutionIn Fig. ABD is a triangle right angled at A and AC ⊥ BD show that
(i) AB2=BC.BD , (ii) AC2=BC.DC , (iii) AD2=BD.CD
View SolutionSolve the following sub question in Delta ABD, angle BAD = 90^(@) seg AC bot hypo BD, B - C- D show that (i) AB^(2) = BC : BD (ii) AD^(2) = BD : CD
View Solution△ABC ಯಲ್ಲಿ AD⊥BC ಮತ್ತು AD2=BDxCD ಆಗಿದೆ. ಹಾಗಾದರೆ AB2+AC2=(BD+CD)2 ಎಂದು ಸಾಧಿಸಿ.
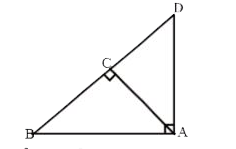
View SolutionABD is a triangle right angled at A and AC ⊥ BD Show that
(i) AB2 = BC .BD.
(ii) AC2 = BC.DC
(iii) AD2 = BD .CD.
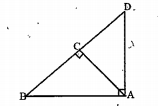
View SolutionABD is a triangle right angled at A andAC⊥BD.Showthat i)AB2=BC⋅BD ii)AC2=BC⋅DC iii) AD2=BD⋅CD
View SolutionIn triangle ABC , AD bisects angle A and intersects BC at D. If BC = a ,AC = b and AB = c, then BD = ? त्रिभुज ABC में, AD कोण A को समद्विभाजित करता है तथा BC को D पर काटता है | यदि BC = a, AC = b और AB = c है, तो BD = ?
View SolutionIn triangle ABC , angle A is a right angle. The lengths of AC and BC 6 cm and 10 cm respectively. Point D is on AB such that BD = 4 cm. What is the length of CD? त्रिभुज ABC में, कोण A समकोण है | AC और BC की लंबाई क्रमशः 6 सेमी और 10 सेमी है | बिंदु D, AB पर इस प्रकार स्थित है कि BD = 4 सेमी है | CD की लंबाई ज्ञात करें |
View Solution
