In the given figure, ADDB=AEEC and ∠ADE=∠ACB. Prove that ΔABC is an isosceles triangle.
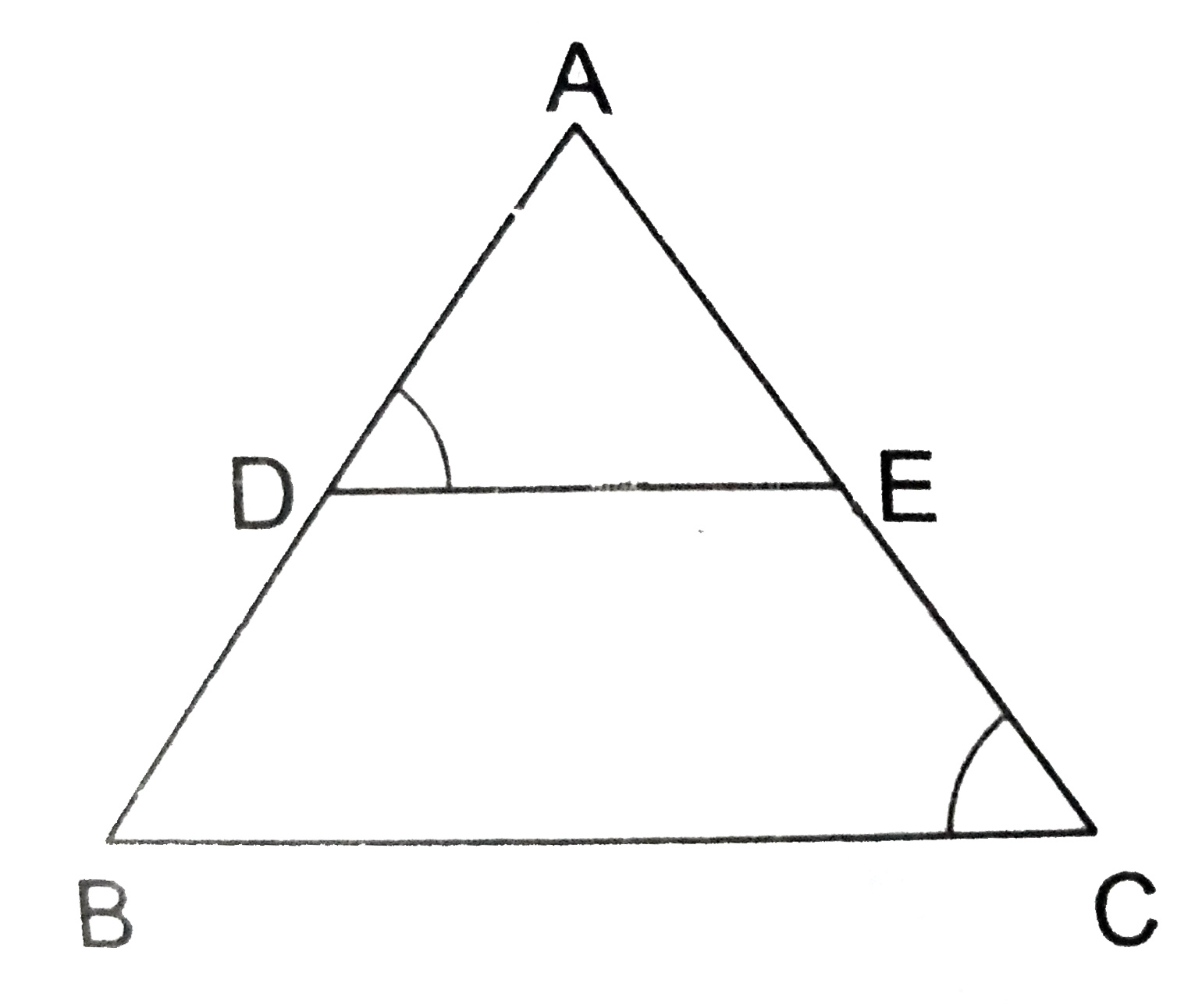
We have,
ADDB=AEEC⇒DE∣∣BC [ by the convrse of Thale's theorem]
∴∠ADE=∠ABC (crossponding ∠).
But, ∠ADE=∠ACB (give) .
∴∠ABC=∠ACB.
So, AB=AC [ sides opposite to equal angles.]
Hence, ΔABC is an isosceles triangle.
Similar Questions
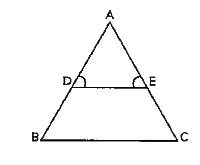
In the figure, ∠D=∠EandADDB=AEEC, prove that ΔBAC is an isosceles triangle
View SolutionIn the given figure , if AB = BC , ∠BAD=∠CAE then prove that △ADE is an isosceles triangle .

View SolutionIn the figure, ∠D=∠E and ADDB=AEEC, prove that BAC is an isosceles triangle.

View SolutionIn the given figure, ∠1=∠2andACBD=CBCE prove that ΔACB~ΔDCE.

View SolutionIn the given figure, DE||BC and ADDB=23if AE=3.7 cm , find EC.

View SolutionIn the given figure, AD = AE and AD2=BD×EC prove that: triangles ABD and CAE are similar.
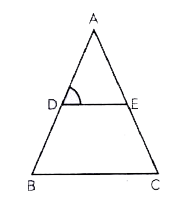
View SolutionIn the given figure, if ∠D=∠C, then it is true that △ADE~△ACB? Why?
View SolutionIn the given figure, if ∠ADE=∠B, show that ΔADE~ΔABC. If AD=3.8cm,AE=3.6cm,BE=2.1cm,andBC=4.2cm, find DE.
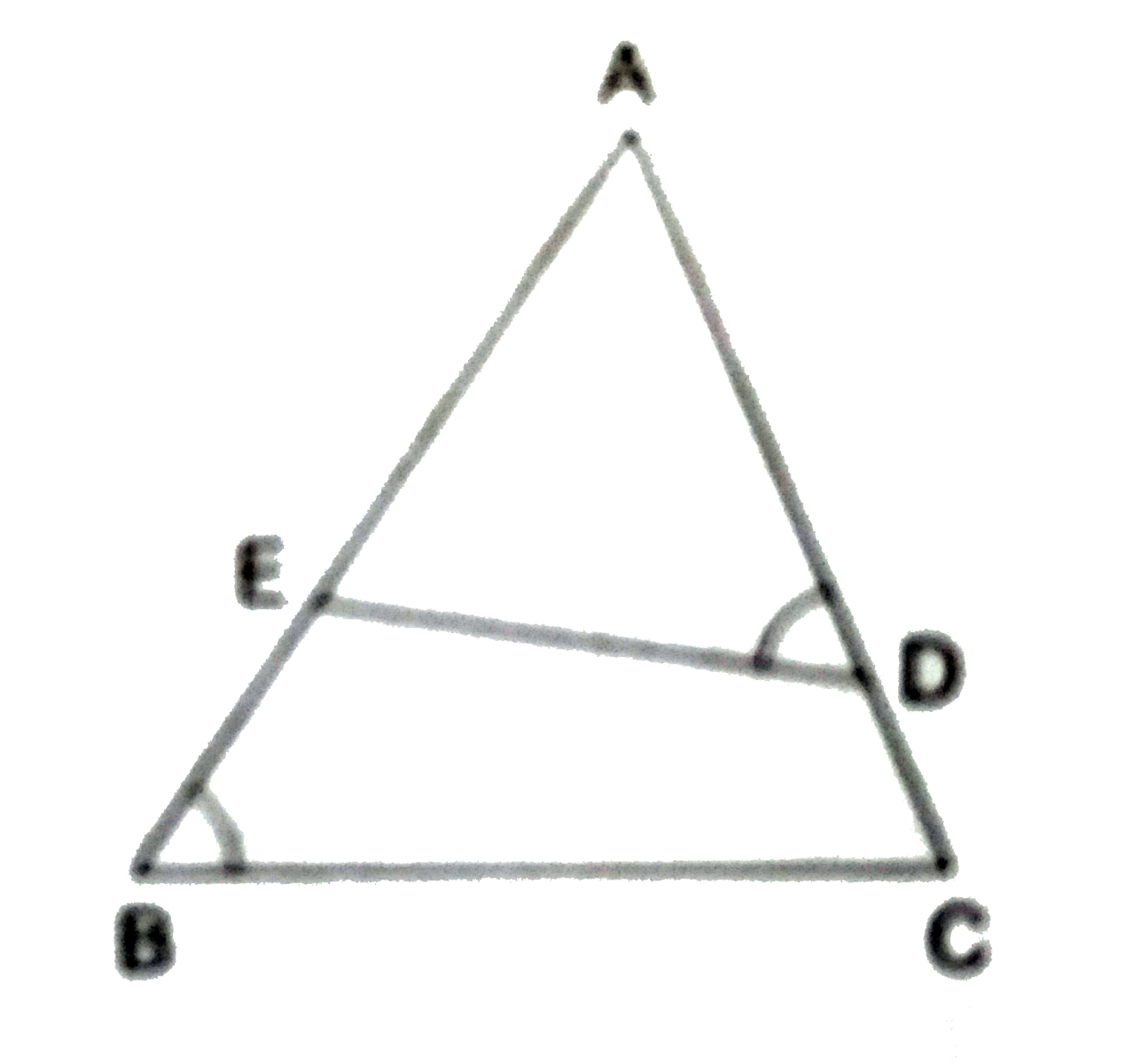
View SolutionIn the given figure if DE∣∣BC then prove that ABDB=ACECandADAB=AEAC
View SolutionIn the given figure, ABC is a triangle, right angled at B. If BCDE is a square on side BC and ACFG is a square on AC, prove that AD = FB.
View Solution