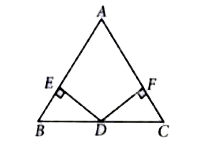
In an equilateral triangle ABC, if AD⊥BC then which of the following is true?
A
2AB2=3AD2
B
4AB2=3AD2
C
3AB2=4AD2
D
3AB2=2AD2
Video Solution
Text Solution
The correct Answer is:C
AB2=BD2+AD2
=(12AB)2+AD2=14AB2+AD2
⇒34AB2=AD2⇒3AB2=4AD2

|
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:MULTPILE-CHOICE QUESTIONS (MCQ) ( MATCHING OF COLUMNS)
Explore 1 Video
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Test Yourself
Explore 20 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Exercise 7E
Explore 30 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
Knowledge Check
In an equilateral ΔABCif AD⊥BC, then
A2AB2=3AD2B3AB2=4AD2C5AB2=6AD2D4AB2=5AD2In the given figure, AB = BC, AD = CD. Then, which of the following is true?
 A∠ADE=90∘BAE=ECCBoth (a) and (b)DAE=BC
A∠ADE=90∘BAE=ECCBoth (a) and (b)DAE=BCIn a △ABC,AB = AC and AD⊥BC, then :
AAB<ADBAB>ADCAB=ADDAB≤AD
AD is an altitude of an equilateral triangle ABC. On AD as base, another equilateral triangle ADE is constructed. Prove that Area ( triangle ADE ): Area ( triangle ABC )=3:4.
View SolutionIn the given figure, PA⊥AB, QB⊥AB and PA=QB.
Which of the following is true?

View SolutionΔABC is an equilateral triangle such that AD⊥ BC, then AD2=
View SolutionIn an equilateral triangle ABC of side 10cm, the side BC is trisected at D. Then the length (in cm) of AD is
View SolutionIn an equilateral triangle ABC, the side BC is trisected at D. Find the value of AD2 :
View Solution