
Using the graph showin in figure, for stopping potential versus the incident frequency of photon, calculate planck's constant.
We know that slope V0v graph for photoelectric effect is he. As per graph, slope:
he=1.23V(8−5)×1014Hz=0.41×10−14Vs
∴Planck.s constant h=e×slope
=(1.6×10−19)×(0.41×10−14)
=6.56×10−34Js
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTERBook:U-LIKE SERIESChapter:DUAL NATURE OF RADIATION AND MATTERExercise:LONG ANSWER QUESTIONS
Explore 19 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:U-LIKE SERIESChapter:DUAL NATURE OF RADIATION AND MATTERExercise:SELF ASSESSMENT TEST SECTION-A (MULTIPLE CHOICE QUESTIONS)
Explore 6 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:U-LIKE SERIESChapter:DUAL NATURE OF RADIATION AND MATTERExercise:VERY SHORT ANSWER QUESTIONS
Explore 34 Videos
- CURRENT ELECTRICITY Book:U-LIKE SERIESChapter:CURRENT ELECTRICITY Exercise:SELF ASSESSMENT TEST (SECTION C )
Explore 3 Videos
- ELECTRIC CHARGES AND FIELDS Book:U-LIKE SERIESChapter:ELECTRIC CHARGES AND FIELDS Exercise:SELF ASSESSMENT TEST (SECTION-B) (VERY SHORT ANSWER QUESTIONS)
Explore 4 Videos
Similar Questions
(a) Why photoelectric effect cannot be explained on the basis of wave nature of light ? Give reasons.
(b) Write the basis features of photon picture of electromagnetic radiation on which einstein's photoelectric equation is based.
View SolutionMomentum of a photon is 3.3×10−28kg ms−1. Its frequency will be
View SolutionName the phenomenon which shows the quantum nature of electromagnetic radiation.
View SolutionState Kirchhoff's rules of current distribution in an electrical network. Using these rules determine the value of the current I1 in the electric circuit of Fig.
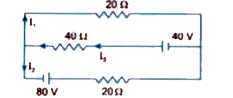
View SolutionThree small , identical point charges lie on the circumference of a circle forming an equilateral triangle.Calculate the value of electric field at the centre of circle.
View SolutionUsing the graph shown in fig for stopping potential vs the incident frequency of photons, calculate Planck's constant.
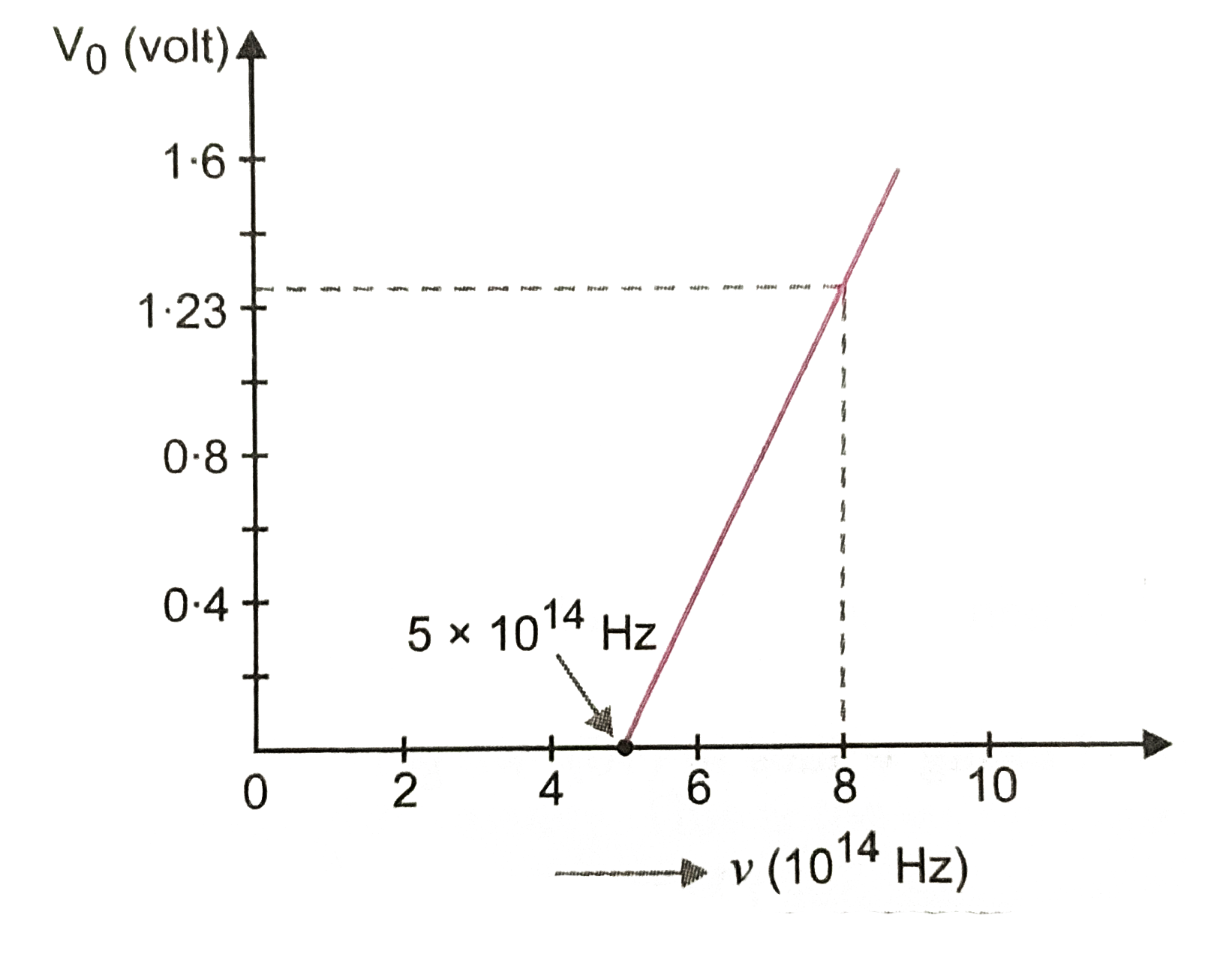
View SolutionDraw a graph showing the variation of stopping potential with frequency of the incident on a metal plate. How can the value of Planck's constant be determined from this graph?
View SolutionIn photo electric effect, the slope of the straight line graph between stopping potential and frequency of the incident light gives the ratio of Planck's constant to
View SolutionThe slope of the stopping potential versus frequency graph for photoelectric effect is equal to:
View SolutionGraph of stopping potential for most energetic emitted photoelectron (VS) with frequency of incident radiation on metal is given below.

The value of ABBC, in graph is
(h=Planck's constant, e = electronic charge)
View SolutionIn a photoelectric experiment, the graph of frequency v of incident light (in Hz) and stopping potential V (in V) is as shown in the figure. Planck's constant is (e is the elementary charge)
View SolutionA photon of frequency 1.5xx10^(15) Hz is incident on a metal surface of work function 1.672 eV. Calculate the stopping potential.
View SolutionIn photoelectric effect the slope of stop of stopping potential versus frequency of incident light for a given surface will be
View SolutionIn a photoelectric experiment, the graph of frequency v of incident light (in Hz) and stopping potential V (in V) is as shown in the figure. Planck's constant is (e is the elementary charge)
View SolutionUsing the graph as in figure for stopping potential vs the incident frequency of photons. Calculate plank's constant.
View SolutionDraw a graph showing the variation of stopping potential with frequency of incident radiation Mark the threshold frequency in the figure.
View Solution

