The set of value of the θ satisfying the inequation 2sin2θ−5sinθ+2>0, where 0<θ<2π, is
A
(0,π6)∪(5π6,2π)
B
[0,π6]∪[5π6,2π]
C
[0,π3]∪[2π3,2π]
D
None of these
Video Solution
Text Solution
The correct Answer is:a
Since, 2sin2θ−5sinθ+2>0
⇒(2sinθ−1)(sinθ−2)>0
[where,(sinθ−2)<0,Aaθ∈R]
∴ (2sinθ−1)<0
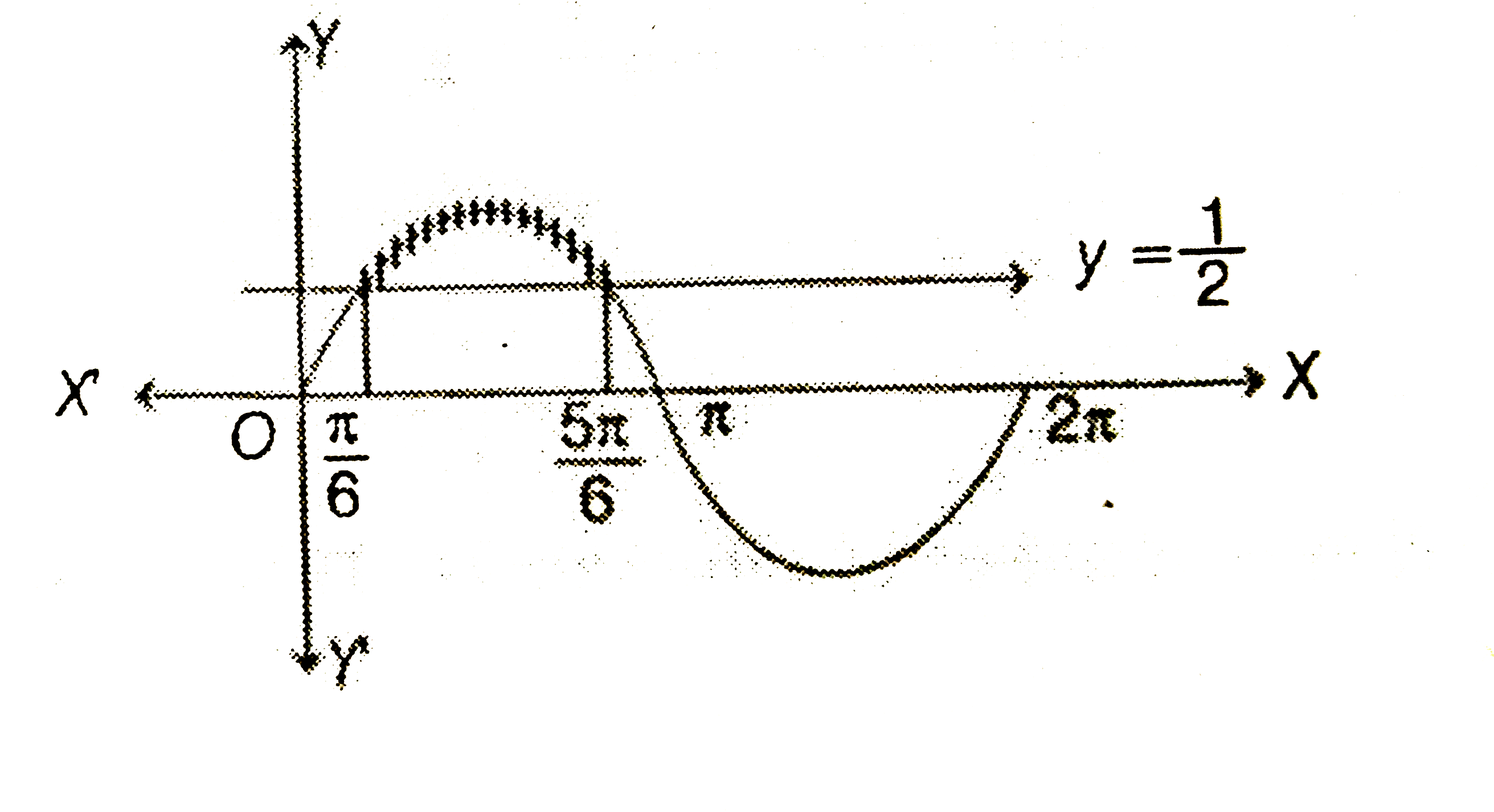
⇒sinθ<12
∴ From the graph,θ∈(0,πθ)∪((5π6,2π)
|
Similar Questions
Knowledge Check
The set of values of θ satisfying the inequatioin 2sin2θ−5sinθ+2>0, where o<θ<2π, is
A[0,π6]∪[5π6,2π]B[0,π6]∪[5π6,2π]C[0,π3]∪[2π3,2π]DNone of theseValue(s) of θ satisfying the equation
sin7θ=sin4θ−sinθ, where 0<θ<(π/2), areAπ/9,π/4Bπ/3,π/9Cπ/6,π/9Dπ/3,π/4The values of θ satisfying sin7θ=sin4θ−sinθ and 0<θ<π2 are
Aπ9,π4Bπ3,π9Cπ6,π9Dπ3,π4
If 2sin2θ−5sinθ+2>0,θ∈(0,2π), thenθ∈ :
View SolutionThe number of values of θ satisfying the equation sinθ+sin5θ=sin3θ such that θ∈[0,π] is
View SolutionThe value of θ(0<a<π2) satisfying the equation sin2θ–2cosθ+14==0 is.
View SolutionThere exist a value of θ between 0 and 2π that satisfies the equaition sin4θ−2sin2θ+1=0
View SolutionThe values of θ satisfying sin7θ=sin4θ−sinθ and 0<θ<π2 are
View Solution
