Let L1andL2 be two lines intersecting at P If A1,B1,C1 are points on L1,A2,B2,C2,D2,E2 are points on L2 and if none of these coincides with P, then the number of triangles formed by these 8 points is
56
55
46
45
The correct Answer is:D
Step by step video, text & image solution for Let L_1 and L_2 be two lines intersecting at P If A_1,B_1,C_1 are points on L_1,A_2, B_2,C_2,D_2,E_2 are points on L_2 and if none of these coincides with P, then the number of triangles formed by these 8 points is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONSBook:OBJECTIVE RD SHARMAChapter:PERMUTATIONS AND COMBINATIONSExercise:Exercise
Explore 136 Videos
- PARABOLABook:OBJECTIVE RD SHARMAChapter:PARABOLAExercise:Chapter Test
Explore 30 Videos
- PROBABILITY Book:OBJECTIVE RD SHARMAChapter:PROBABILITY Exercise:Chapter Test
Explore 45 Videos
Similar Questions
The straight lines l1,,l2&l3, are parallel & lie in the same plane. A total of m points are taken on the line l1, n points on l2,&k points on l3. How many maximum number of triangles are there whose vertices are at these points ?
View SolutionLet l1andl2 be the two skew lines. If P, Q are two distinct points on l1 and R, S are two distinct points on l2, then prove that PR cannot be parallel to QS.
View Solution
Knowledge Check
Three straight lines L1,L2 and L3 are parallel and lie in the same plane. A total of m points are taken on L1, n points on. L2, K points on L3. The maximum number of triangles formed with vertices at these points are
A^(m+n+k)C3B^(m+n+k)C3−mC3−nC3C^(m+n+k)C3+mC3+nC3DNone of theseThe area of triangle formed by the lines l1andl2 and the x-axis is:
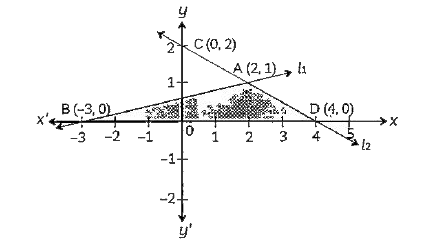 A7 sq. unitsB92 sq.unitsC72 sq.unitsD4 sq. units
A7 sq. unitsB92 sq.unitsC72 sq.unitsD4 sq. unitsThe straight lines I1,I2,I3 are paralled and lie in the same plane. A total number of m point are taken on I1,n points on I2, k points on I3. The maximum number of triangles formed with vertices at these points are
AmC3×nC3×kC3B^(m+n+k)C3−(mC3+nC3+kC3)Cm+n+kC3Dnone of the above
Consider three planes P1:x−y+z=1, P2:x+y−z=−1 and P3:x−3y+3z=2 Let L1,L2 and L3 be the lines of intersection of the planes P2andP3, P3andP1 and P1andP2 respectively.Statement 1: At least two of the lines L1,L2andL3 are non-parallel The three planes do not have a common point
View SolutionIf the line of intersection of plane
P : 2x + y + z = 2 with xy plane is L1,
with zx plane is L2 and with yz plane is
L3 then the area of triangle formed by
lines L1,L2,L3 is △, then the value of △2 is equal to
View SolutionLet L1=0 and L2=0 be two intersecting straight lines. Then the number of points, whose distance from L1 is 2 units and from L2 is 5 units is (i)1 (ii)0 (iii)4 (iv)∞
View SolutionThe straight lines I1,I2,I3 are paralled and lie in the same plane. A total number of m point are taken on I1,n points on I2, k points on I3. The maximum number of triangles formed with vertices at these points are
View SolutionThe straight lines l2||l2||l3 and lies in the same plane A total of m points are taken on l1 ,n points on l2 and k point on l3, then maximum number of triangles formed with vertices at these points are
View Solution
