Electric potential difference between the positive plate and halfway point between the two parallel plates of a fully charged capacitor is
Zero
One half of the total potential difference between the two plates
One quarter of the total potential difference between the two plates
None of the above
The correct Answer is:B
To solve the problem of finding the electric potential difference between the positive plate and the halfway point between the two parallel plates of a fully charged capacitor, we can follow these steps:
1. Understand the Setup:
- A capacitor consists of two parallel plates: one positively charged and the other negatively charged. Let's denote the total potential difference between the two plates as V.
2. Identify the Halfway Point:
- The halfway point between the two plates is located at the midpoint of the distance separating the plates.
3. Electric Field in a Capacitor:
- The electric field E between the plates of a parallel plate capacitor is uniform and can be expressed as:
E=Vd
where d is the distance between the plates.
4. Potential Difference Calculation:
- The potential difference V′ between the positive plate and the halfway point can be calculated using the formula for potential difference, which is the product of the electric field and the distance:
V′=E⋅(d2)
- Substituting the expression for E:
V′=(Vd)⋅(d2)
- Simplifying this gives:
V′=V2
5. Conclusion:
- The electric potential difference between the positive plate and the halfway point is half of the total potential difference V. Therefore, the answer is:
Electric potential difference=V2
Final Answer:
The electric potential difference between the positive plate and the halfway point between the two parallel plates of a fully charged capacitor is one half of the total potential difference between the two plates.
- A capacitor consists of two parallel plates: one positively charged and the other negatively charged. Let's denote the total potential difference between the two plates as V.
- The halfway point between the two plates is located at the midpoint of the distance separating the plates.
- The electric field E between the plates of a parallel plate capacitor is uniform and can be expressed as:
E=Vd
where d is the distance between the plates.
- The potential difference V′ between the positive plate and the halfway point can be calculated using the formula for potential difference, which is the product of the electric field and the distance:
V′=E⋅(d2)
- Substituting the expression for E:
V′=(Vd)⋅(d2)
- Simplifying this gives:
V′=V2
- The electric potential difference between the positive plate and the halfway point is half of the total potential difference V. Therefore, the answer is:
Electric potential difference=V2
The electric potential difference between the positive plate and the halfway point between the two parallel plates of a fully charged capacitor is one half of the total potential difference between the two plates.
Topper's Solved these Questions
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
12 Videos
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTIONS (LINKED COMPREHENSION)
8 Videos
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PROBLEMS
48 Videos
- ALL ABOUT ATOMS BOOK - RESNICK AND HALLIDAYCHAPTER - ALL ABOUT ATOMS EXERCISE - CHECKPOINT
1 Video
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )
4 Videos
Similar Questions
A dielectric slab of thickness d is inserted in a parallel plate capacitor whose negative plate is at x=0 and positive plate is at x=3d. The slab is equidistant from the plates. The capacitor is given some charge. As one goes from 0 to 3d(1998).
View SolutionConsider a parallel plate capacitor originally with a charge q0 capacitance C0 and potential difference ΔV0 There is an electrostatic force of magnitude F0 between the plates and the capacitor has a stored energy U0. The terminals of the capacitor are connected to another capacitor of same capacitance and charge.
A dielectric slab with ke>1 is inserted between the plates of the first capacitor . Which quantity decreases?
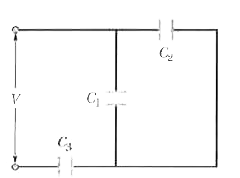
View SolutionIn Fig. 25-25 C1=10.0μF,C2=5.0μFandC3=4.0μF What is the change in their equivalent capacitance if (a) capacitors 1 and 2 are interchanged and (separately) (B) capacitors 1 and 3 are interchanged?
View SolutionDoes the cutoff wavelength λmin of the continous x- ray spectrum increse decrease or remain the same if you (a) increase the kinetic energy of the electrons that strike the x ray target (b ) allow the electrons to strike a thin foil rather than a thick block of the target material ,(c ) change the target to an element of higher atomic number ?
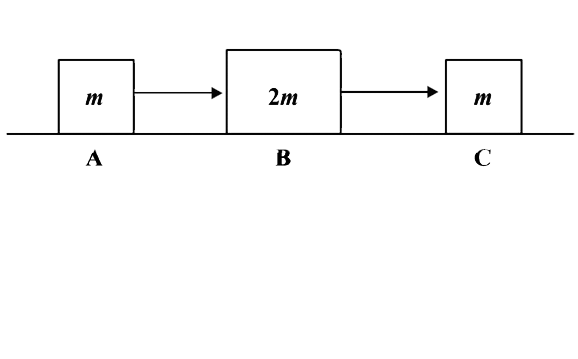
View SolutionThere object A,B and C are kept is a straing line a fritionlas horizental surface . These have masses have increase on 2m and m repectively . The object A move toward B with a speed 9 m//s and makes as electic collision with a there after B makes complately inclesis with C . All motion over on the same strangth line . Find the first speed of the object C
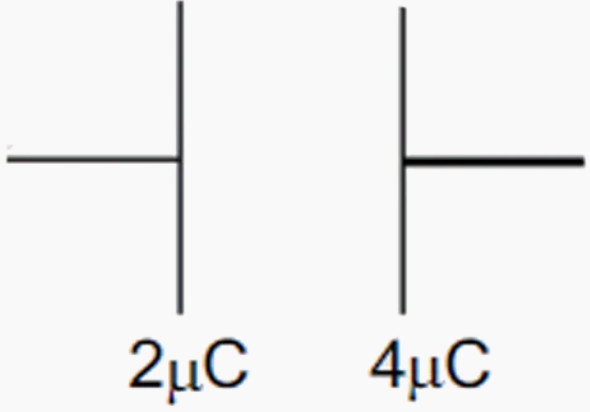
View SolutionIn a parallel plate capacitor of capacitor 1μF two plates are given charges 2μC and 4μC the potential difference between the plates of the capacitor is
View SolutionA parallel plate air capacitor is charged to a potential difference of V volts. After disconnecting the charging battery the distance between the plates of the capacitor is increased using an isulating handle. As a result the potential difference between the plates
View SolutionA parallel plate air capacitor is charged to a potential difference of V volts. After disconnecting the charging battery the distance between the plates of the capacitor is increased using an insulating handle. As a result the potential difference between the plates:-
View SolutionThe distance between the two plates of an isolated charged parallel plate air capacitor is increased. The potential difference between the plates will……………………..
View SolutionA parallel plate capacitor is charged to a potential difference of V volts. After disconnecting the charging battery the distance between the plates of the capacitor is increased using an insulating handle. As a result the potential difference between the plates
View Solutionसमांतर - प्लेट संधारित्र की धारिता , प्लेटों के बीच विभवांतर पर निर्भर करती है।
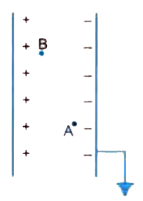
View SolutionIn a parallel plate capacitor the potential difference of 100 V is manitianed between the plates. If distance between the plates be 5mm, what will be the electric field at points A and B ?
View SolutionIn a parallel plate capacitor of capacitor 1μF two plates are given charges 2μC and 4μC the potential difference between the plates of the capacitor is
_2019_CBT2_E01_002_Q01.png)
View SolutionA parallel plate air capacitor is charged to a potential difference of V volts. After disconnecting the charging battery the distance between the plates of the capacitor is increased using an isulating handle. As a result the potential difference between the plates
View SolutionA parallel plate air capacitor is charged to a potential difference of V volts. After disconnecting the charging battery the distance between the plates of the capacitor is increased using an isulating handle. As a result the potential difference between the plates
View Solution

