If α,β,γ are the cube roots of p, then for any x,y,z xα+yβ+zγxβ+yγ+zα =
The correct Answer is:ω2
xα+yβ+zγzβ+yγ+zα=x(p)1/3+y(p)1/3+ω+z(p)1/3ω2ω2x(+yω+zω2)x(p)1/3ω2+y(p)1/3ω3+z(p)1/3ωω2(xω+yω2+z)
ω2(x+yω+zω2)x+yω+zω2=ω
Topper's Solved these Questions
- COMPLEX NUMBERSBook:IIT JEE PREVIOUS YEARChapter:COMPLEX NUMBERSExercise:TOPIC 2 CONJUGATE AND MODULUS OF A COMPLEX NUMBER (TRUE/FALSE )
Explore 3 Videos
- COMPLEX NUMBERSBook:IIT JEE PREVIOUS YEARChapter:COMPLEX NUMBERSExercise:TOPIC 2 CONJUGATE AND MODULUS OF A COMPLEX NUMBER (ANALYTICAL & DESCRIPTIVE QUESTIONS )
Explore 10 Videos
- COMPLEX NUMBERSBook:IIT JEE PREVIOUS YEARChapter:COMPLEX NUMBERSExercise:TOPIC 2 CONJUGATE AND MODULUS OF A COMPLEX NUMBER (MATCH THE COLUMNS)
Explore 1 Video
- CIRCLEBook:IIT JEE PREVIOUS YEARChapter:CIRCLEExercise:Topic 5 Integer Answer type Question
Explore 1 Video
- DEFINITE INTEGRATIONBook:IIT JEE PREVIOUS YEARChapter:DEFINITE INTEGRATIONExercise:LIMITS AS THE SUM
Explore 6 Videos
Similar Questions
If three complex numbers are in AP. Then, they lie on a circle in the complex plane .
View SolutionFind the centre and radius of the circle formed by all thepoints represented by z=x+iy satisfying the relation ∣∣∣z−αz−β∣∣∣=k(k≠1), where αandβ are the constant complex numbers given by α=α1+iα2,β=β1+iβ2.
View SolutionMatch the statements of Column I with those of Column II
Here ,z takes values in the complex plane and Im (z) and Re(z) denote respectively , the imaginary part and the real part of z
View SolutionTwo parallel chords of a circle of radius 2 are at a distance √3+1 apart. If the chord subtend angles πkand2πk at the center, where k>0, then the value of [k] is _____
View Solutionlimn→∞((n+1)1/3n4/2+(n+2)1/3n4/3+....+(2n)1/3n4/3) is equal to
View SolutionIf α,β,γ are the cube roots of p, then for any x,y,z xα+yβ+zγxβ+yγ+zα =
View SolutionIf alpha be the real cube root of and beta,gamma be the complex cube roots of m, a real positive number,then for any x,y,z show that (x beta+y gamma+z alpha)/(x gamma+y alpha+z beta)=omega^(2), where omega is a complex cube root of unity.
View SolutionIf alpha,beta,gamma are cube roots of of p<0 then for any real x,y,z;(x alpha+y beta+z gamma)/(x beta+y gamma+z alpha)=
View SolutionIf alpha,beta,gamma are the cube roots of p then for any x,y and z(x alpha+y beta+z gamma)/(x beta+y gamma+z alpha) is
View SolutionProve that
∣∣ ∣ ∣∣1x+αy+z−α1t+β+x−β1z+γx+y−γ∣∣ ∣ ∣∣=0
View SolutionIf alpha , beta , gamma are cube roots of p lt 0 , then for any x , y,z (alpha^(2)x^(2)+beta^(2)y^(2)+gamma^(2)z^(2))/(beta^(2)x^(2) + gamma^(2)y^(2) + alpha^(2)z^(2)) is
View SolutionLet P(α,β,γ)andQ(1,−1,0) be points such that the mid-point of PQ is R(x,y,z). If x is the AM of αandβ,y is the G.M. of βandγandz is the H.M . Of γandα then :
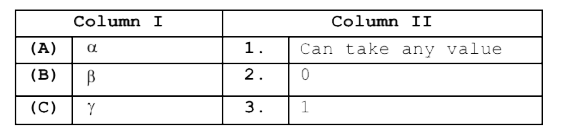
View SolutionIfxtan(θ+α)=ytan(θ+β)=ztan(θ+γ),prove that
x+yx−ysin2(α−β)+y+zy−zsin2(β−γ)+z+xz−xsin2(γ−α)=0
View SolutionIf α,β,γ are the cube roots of a negative number p, then for any three real numbers x,y,z the value of xα+yβ+zγxβ+yγ+zα is
View SolutionIf α,β,γ are the cube roots of p, then for any x,y,z xα+yβ+zγxβ+yγ+zα =
View SolutionIf 1,ω,ω2 are the three cube roots of unity and α,β,γ are the cube roots of p,p<0, then for any x, y, z the expression xα+yβ+zγxβ+yγ+zα=
View Solution
