State the law of radioactive decay.
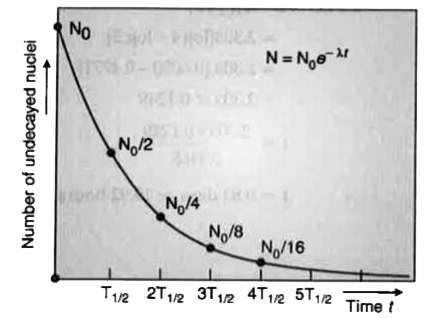
Plot a graph showing the number (N) of undecayed nuclei as a function of time (t) for a given radioactive sample having half life T1/2.
Depict in the plot, the number of undecayed nuclei at (i) t=3T1/2 and (ii) t=5T1/2.Solution in Kannada
The number of nuclei undergoing decay per unit time, at any instant, is proportional to the total number of nuclei in the sample at that instant.
Alternatively :
−dNdt∝N
⇒dNdt=−λN
Similar Questions
Plot a graph showing the variation of undecayed nuclei N versus time t. From the graph, find out how one can determine the half-life and average life of the radioactive nuclei.
View SolutionState the law of radioactive decay. Plot a graph showing the number (N) of undecayed nuclei as a function of time (t) for a given radioactive sample having half-life T_(1/2) . Depict in the plot the number of undecayed nuclei at (i) t= T_(1/2) and (ii) t= 5T_(1/2) .
View Solution(a) The number of nuclei of a given radioactive sample at time t = 0 and t= T are N0 and N0n respectively. Obtain an expression for the half-life T12. of the nuclide in terms of n and T.
(b) Write the basic nuclear process underlying β−-decay of a given radioactive nucleus.
View Solution(a) State the law of radioactive decay. Plot a graph showing the number (N) of undecayed nuclei as a function of time (t) for a given radioactive sample having half-life T12.
Depict in the plot the number of undecayed nucei at (i) t=3T12 and (ii) t=5T12.
(b) The half-life, of a given radioactive nuclide, is 138.6 days. What is the mean life of this nuclide? After how much time will a given sample of this radioactive nuclide get reduced to only 12.5% of its initial value?
View SolutionState the law of radioactive decay. Plot a graph showing the number (N) of undecayed nuclei as a function of time (t) for a given radioactive sample having half life T1/2
Depict in the plot the number of undecayed nuclei at
(i) t=3T1/2 and (ii) t=5T1/2.
View SolutionAt a given instant, there are 25% undecayed radioactive nuclei in a sample. After 10 seconds the number of undecayed nuclei reduces to 12.5%, the mean life of the nuclei is
View SolutionIn a sample of a radioactive substance what fraction of the initial number of nuclei will remain undecayed after a time t=T2 where T=half-life of radioactive substance.
View Solution
