Deduce the condition for balance of a wheatstone's bridge using Kirchoffs rules . Solution in Kannada
Video Solution
Text Solution
Circuit diagram with current direction
Applying KCL and KVL
Arriving final expression R1R2=__
Detailed Answer:
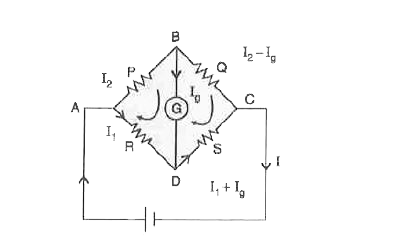
Applying Kirchhoff.s loop law to the closed loop ABCD, we get
Applying Kirchhoff.s loop law to the closed loop BCDB, we get
−(I2−Ig)Q+(I1+Ig)s+IgG=0
In case of balanced Wheatstone bridge, no current flows through the galvanometer i.e.,
Hence equation (1) becomes
−I2P+I1R=0
I1R=I2P
I1I2=PQ
Similarly equation (2) becomes −I2Q+I1S=0
I1S=I2Q
I1I2=QS
For equation (3) and (4) we get
PQ=QS
Or PQ=RS.
|
Similar Questions
Deduce the condition for balance of a wheatstone's bridge using Kirchoffs rules .
View SolutionDeduce the condition for balance of a wheatstone's bridge using Kirchoffs rules .
View SolutionIn a balanced Wheatstone's bridge, if the position of the galvanometer and cell is interchanged then the balanced condition will
View SolutionWhat is the condition of balanced wheatstone's bridge?
View SolutionWhen a wheatstone's bridge is said to be balanced ?
View SolutionWhat is mean by balanced wheatstone's bridge ?
View SolutionApply Kirchoff's laws of current electricity to establish the condition of a balanced Wheatstone's bridge.
View Solution

