3 resistors R1,R2andR3 are connected in series to a battery. Draw the circuit diagram showing the arrangement. Derive an expression for the equivalent resistance of the combination.
(b) Resistors are given as R1=10Ω,R2=20ΩandR3=30Ω. Calculate the effective resistance when they are connected in series . Also calculate the current flowing when the combination is connected to a 6V battery.
(b) Here R1=10Ω,R2=20ΩandR3=30Ω
∴ Effective resistance in series R=R1+R2+R3=10+20+30=60Ω
As voltage of battery V=6V
∴ Current flowing in series combination of resistors
I=VR=6V60Ω=0.1A
Similar Questions
(a) Resistors given as R1,R2andR3 are connected in series to a battery V. Draw the circuit diagram showing the arrangement. Derive an expression for the equivalent resistance of the combination.
(b) If R1=10Ω,R2=20ΩandR3=30Ω, calculate the effective resistance when they are connected in series to a battery of 6 V. Also find the current flowing in the circuit.
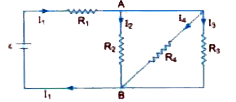
View SolutionIn the circuit shown , R1=4Ω,R2=R3=15Ω,R4=30Ω and ε=10V . Calculate the equivalent resistance of the circuit and the current in each resistor.
View Solution
Knowledge Check
Given Resistance R1=(8±0.4)Ωand Resistence, R2=(8±0.6)Ω What is the net resistence when R1 and R2 are connected in series?
A(16±0.4Ω)B(3.45±0.3)ΩC(3.45±0.4)ΩD(3.45±0.5)ΩThe equivalent resistance of two resistor connected in series is 6Ω and their equivalent resistance is 43Ω. What are the values of resistances ?
A4Ω,6ΩB8Ω,1ΩC4Ω,2ΩD6Ω,2Ω
Five equal resistors each of RΩ are connected in a network. Calculate the equivalent resistance between the points A and B.

View SolutionIn the circuit shown, R1=4Ω,R2=R3=15Ω,R4=30ΩandE=10V. Caculate the equivalent resistance of te circuit and the current in each resistor.
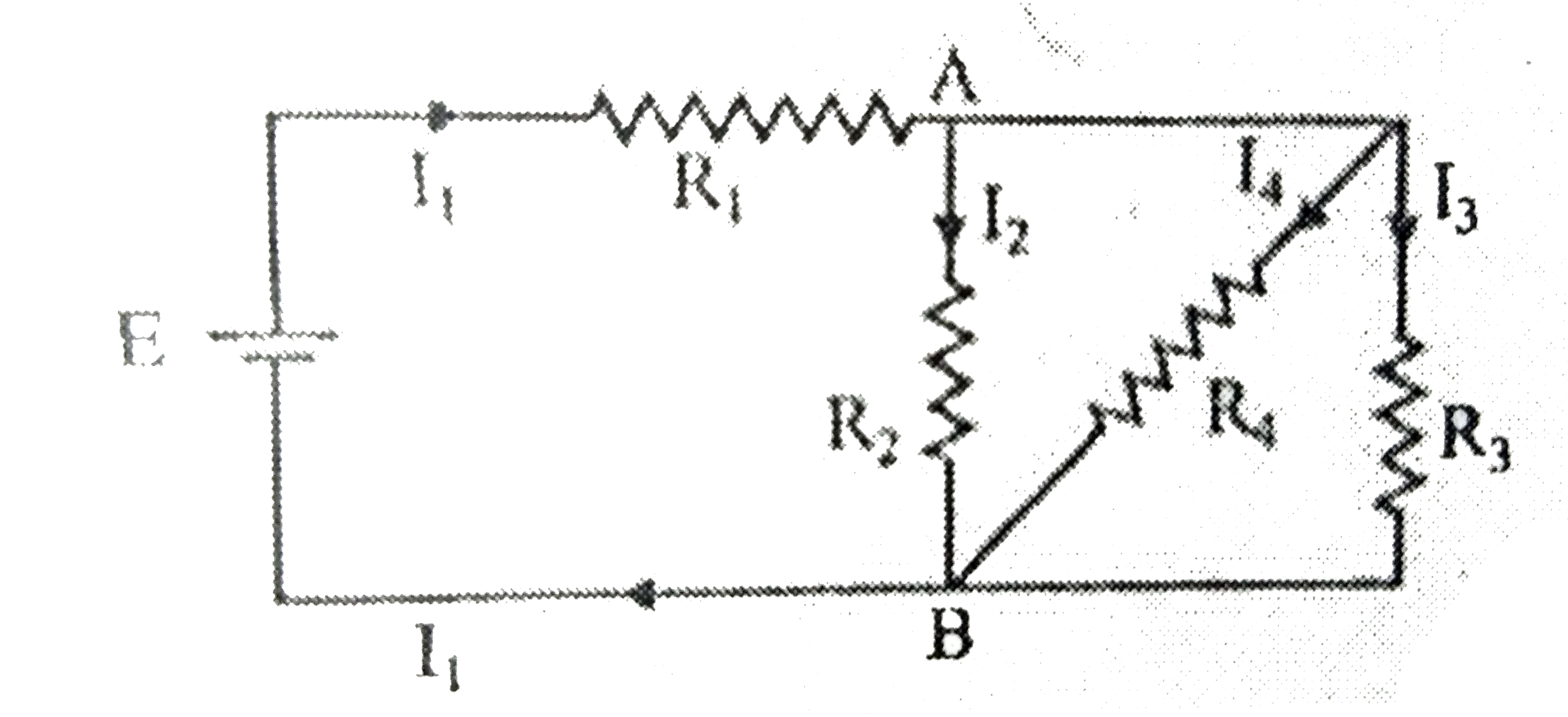
View SolutionIn the circuit R1=4Ω,R2=R3=15ΩR4=30ΩandE=10V Calculate the equivalent resistance of the circuit and current in each resistor
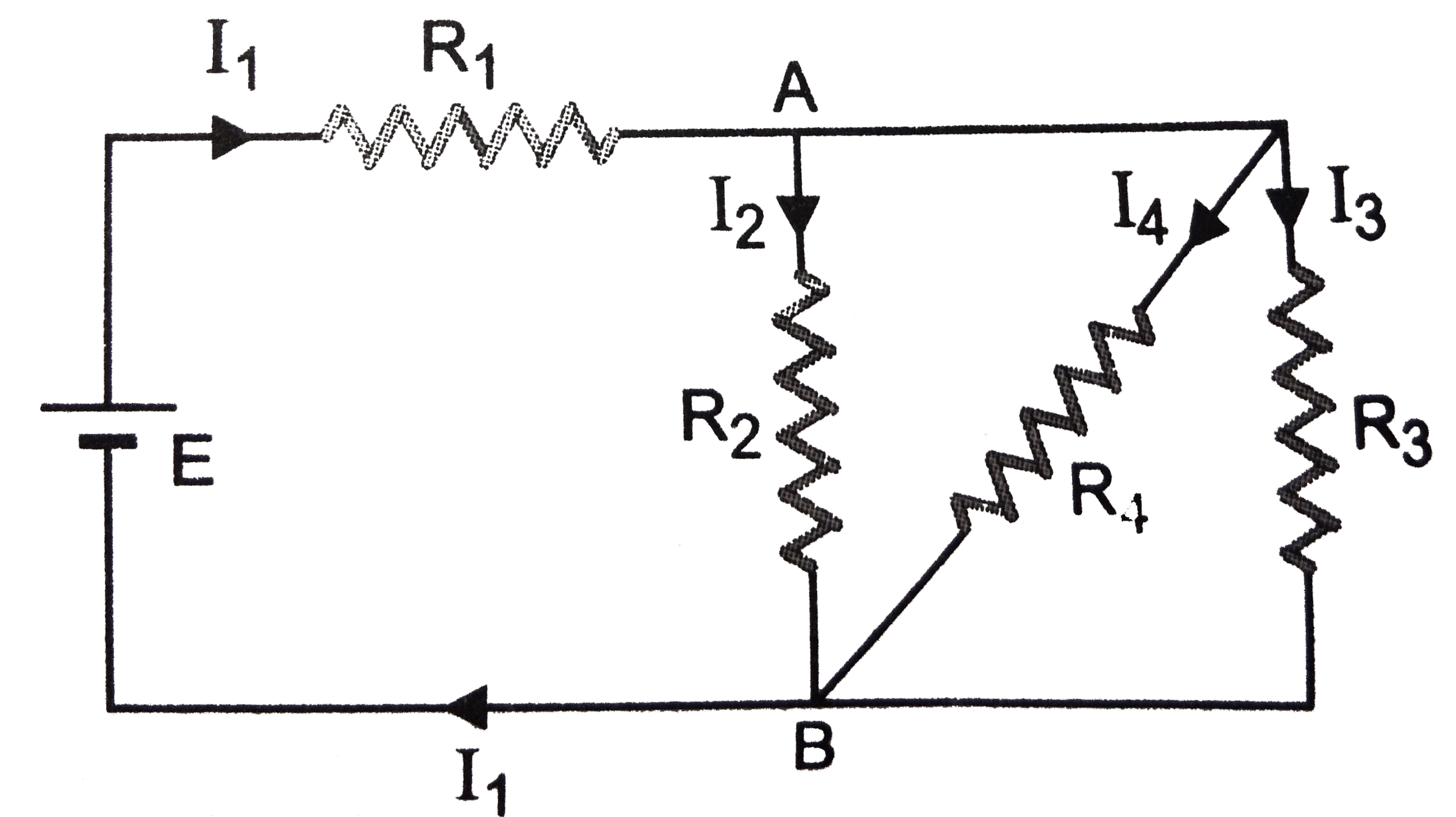
View SolutionThree resistors of resistances R1,R2andR3 are connected in (i) series and (ii) parallel. Write expression for the equivalent resistance of the combination in each case.
(b) Two identical resistance of 12Ω each are connected to a battery of 3V. Calculate the ratio of the power consumed by the resulting combinations with minimum resistance and maximum resistance.
View SolutionIn the circuit shown, R1=2Ω,R2=R3=10ΩandE=6V. Work out the equivalent resistance of the circuit and the current in each resistor.
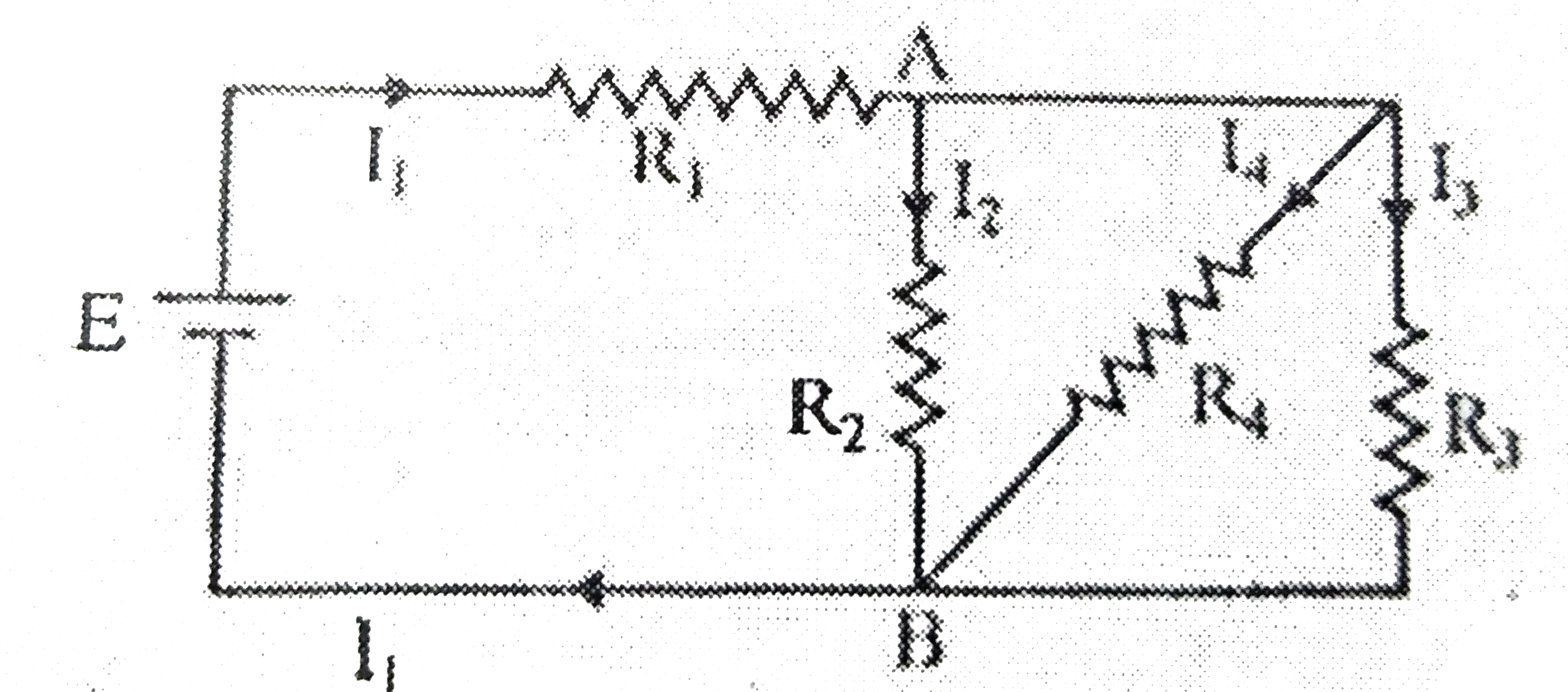
View SolutionResistances R1,R2,R3,R4,R5,andR6 are connected with a 6V battery with internal resistacne 1Ω as shown in fig 5.90. Find (a) equivalent resistance and (b) current in each resistacne.
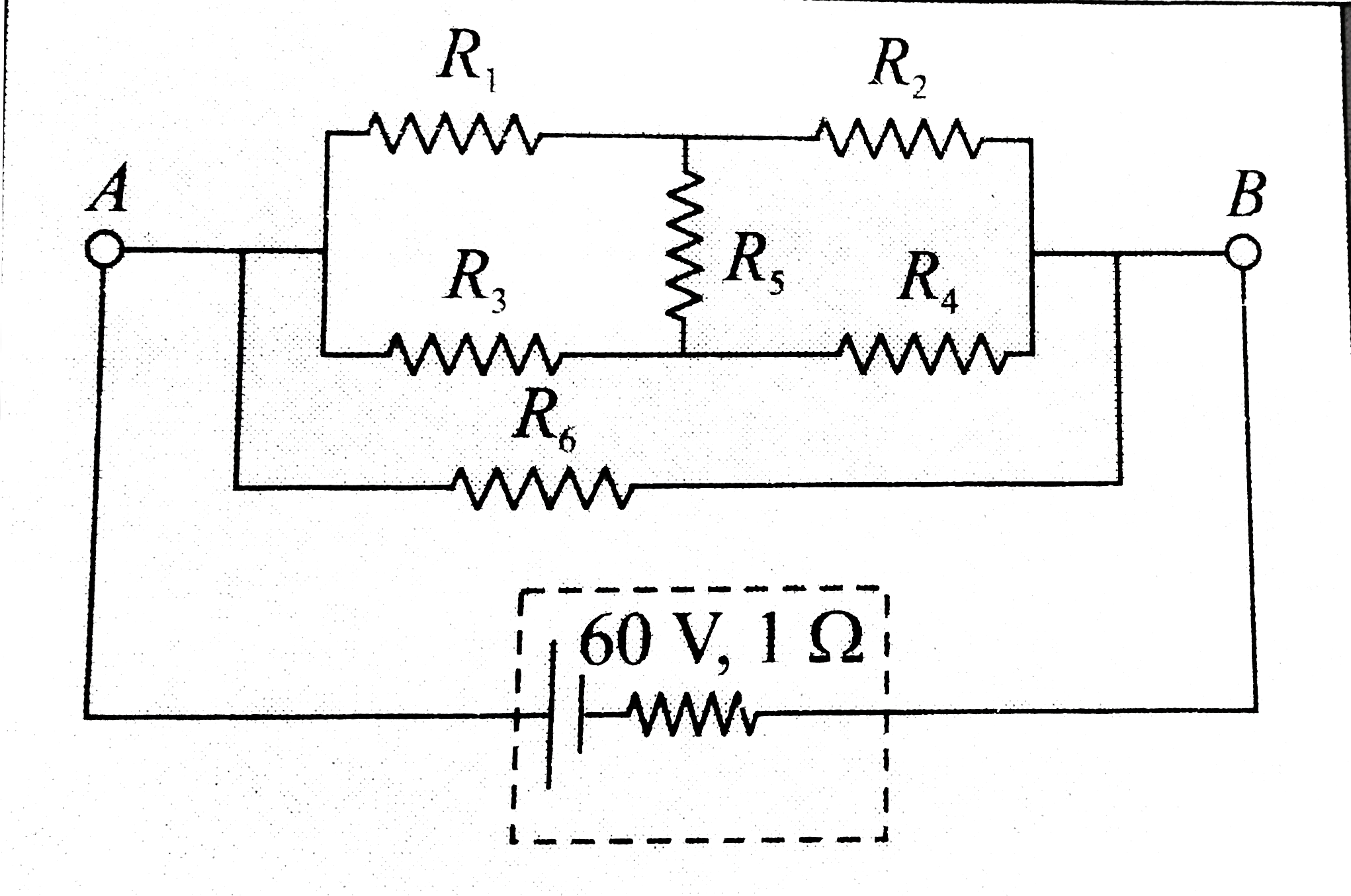
View Solution
