In Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such thatAD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).
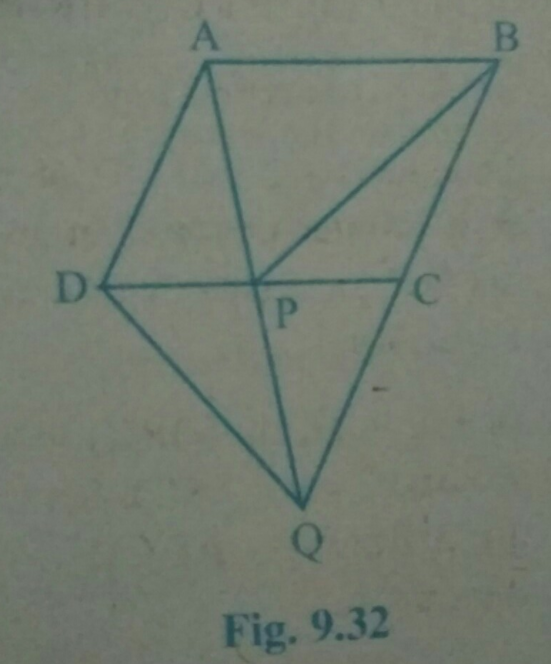
It is given that ABCD is a parallelogram.
AD∣∣BC and AB∣∣DC (Opposite sides of a parallelogram are parallel to each other).
Now, join the points A and C.
Consider △APC and △BPC
△APC and △BPC are lying on the same base PC and between the same parallels PCandAB.
According to Theorem 9.2:
Two triangles on the same base (or equal bases) and between the same parallels are equal in area.
Therefore,Area(△APC)=Area(△BPC) ...(1)
In quadrilateral ACQD, it is given that AD=CQ
Since ABCD is a parallelogram,
AD∣∣BC(Opposite sides of a parallelogram are parallel)
CQ is a line segment that is obtained when line segment BC is produced.
AD∣∣CQ
We have,
AD=CQ and AD∣∣CQ
Hence, ACQD is a parallelogram.
Consider △DCQ and △ACQ
These are on the same base CQ and between the same parallels CQ and AD.
Therefore,
Area(△DCQ)=Area(△ACQ)
Area(△DCQ)−Area(△PQC)=Area(△ACQ)−Area(△PQC)
[Subtracting Area (△PQC) on both sides.]
Area(△DPQ)=Area(△APC) ...(2)
From equations (1) and (2), we obtain
Area(ΔBPC)=Area(ΔDPQ), proved.
Similar Questions
ABCD is a parallelogram whose diagonals AC and BD intersect at O. A Line through O intersects AB at P and DC at Q. Prove that ar(POA)=ar(QOC).
View SolutionABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R, prove that R is a mid-point of BC.
View SolutionABCD is a parallelogram. P is the mid-point of AB.BD and CP intersect at Q such that CQ:QP=3:1. If ar (PBQ)=10 cm2, find the area of parallelogram ABCD
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13AD and Q is a point on BC such that CQ=13BP . Prove that AQCP is a parallelogram.
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that CQ=13BC. Prove that AQCP is a parallelogram.
View SolutionPQRS is a square such that PR and SQ intersect at O. State the measure of ∠POQ.
View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R. Prove that R is a mid-point of BC.
View SolutionIn ABC,D is the mid-point of AB,P is any point of BC.CQPD meets AB in Q . Show that ar(BPQ)=12ar(ABC).
View Solution