आकृति में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए है। यदि AD,BD को O पर प्रतिच्छेद पर तो दर्शाइए कि ar(ΔABC)ar(ΔDBC)=AODO है।
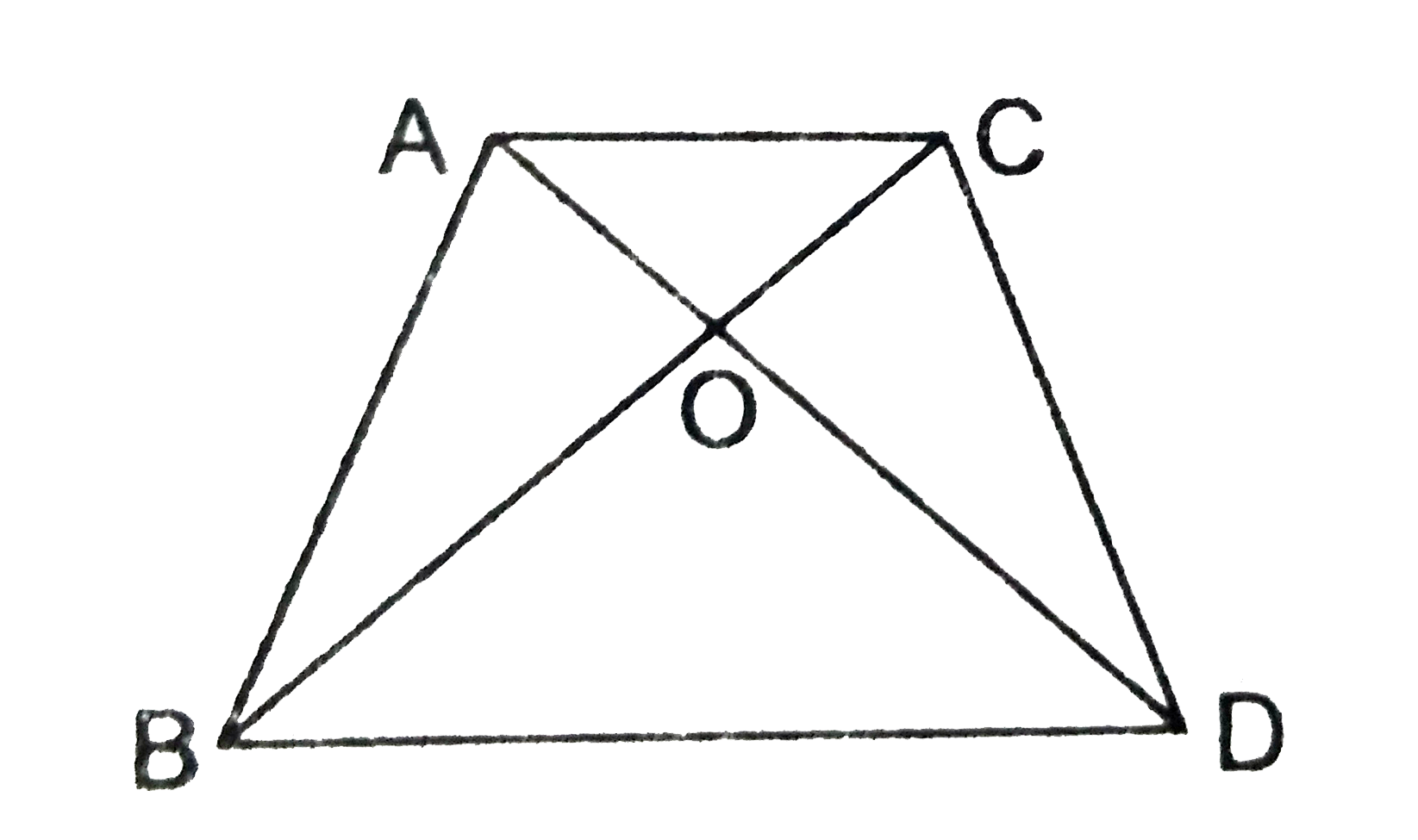
Step by step video & image solution for आकृति में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए है। यदि AD,BD को O पर प्रतिच्छेद पर तो दर्शाइए कि (ar(DeltaABC))/(ar(DeltaDBC))=(AO)/(DO) है। by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
The inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
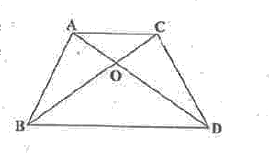
View SolutionIn Fig , ABC and DBC are two triangles on the same base BC. If AD intersects BC,at O , show that ar(ABC)ar(DBC)=AODO
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View SolutionIn the given fig. If DE||BC Find EC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/MATH_241_X_SQP_E01_021_Q01.png" width="80%"gt
View SolutionIn the given figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)=AODO.
View SolutionA circle is inscribed in triangle ABC , touching AB at P, BC at Q and AC at R. If AR=5 cm, RC= 6 cm and AB=12 cm, then perimeter of triangle ABC is: एक वृत्त किसी त्रिभुज ABC में समाहित है जो AB को P पर, BC को Q पर तथा AC को R पर स्पर्श करता है | यदि AR =5 सेमी और AB = 12 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |
View Solution