Establish a relationship to determine the equivalent resistance R of a combination of three resistors having resistances R1,R2 and R3 connected In series. Calculate the equivalent resistance of the combination of three resistors of 2Ω,3Ω and 6Ω joined in parallel. Solution in Kannada
An applied potential V produces current I in the resistors R1,R2 and R3, causing a potential drop V1V2 and V3 respectively through each resistor.
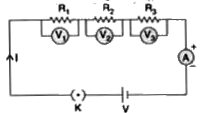
Total Potential ,V=V1+V2+V3
By Ohm.s Law V1=IR1
V2=IR2
V3=IR3
Thus V=IR1+IR2+IR3
=I(R1+R2+R3)
IF R is the equivalent resistance V=IR
Hence IR=I(R1+R2+R3)
R=R1+R2+R3
This proves that overall resistance increases when resistors are connected in series. Three resistors 2Ω,3Ω and Ω, are joined in parallel combination.
Equivalent resistance
1Rp=12+13+16
=2+2+16=66
Rp=1Ω
Similar Questions
Establish a relationship to determine the equivalent resistance R of a combination of three resistors having resistances R1,R2andR3 connected in series.
(b) Calculate the equivalent resistance R of a combination of three resistors of 2Ω,3Ωand6Ω joined in parallel.
View SolutionDerive an expression for the equivalent resistance of three resistors R_(1) R_(2) and R_(3) connected in series.
View SolutionFor the series combination of three resistors establish the relation : R=R_(1)+R_(2)+R_(3) where the symbols have their usual meanings. Calculate the equivalent resistance of the combination of three resistors of 6Omega , 9 Omega and 18 Omega joined in parallel.
View SolutionTwo resistors of resistances R1=(300±3)Ω and R2=(500±4)Ω are connected in series. The equivalent resistance of the series combination is
View SolutionTwo resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
View SolutionThe equivalent resistance of a series combination of two resistors is '9 Omega' and the equivalent resistance of a parallel combination of the same two resistors is 2Ω. Find the resistances of the resistors.
View SolutionTwo resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
View Solution