See the figure here. We have two hollow thin spherical shells A and B of radii R, and R, respectively. Initially as shown in Fig. (i) shell B has a charge + Q which is uniformly distributed over its outer surface but shell B has no charge. At a particular instant the two spherical shells are connected by a thin copper wire as shown in Fig. (ii). After a couple of minutes two spherical shells A and B are disconnected again as shown in Fig. (iii).
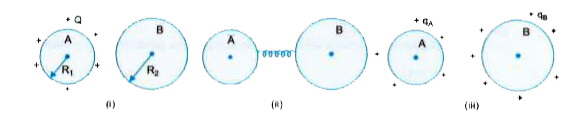
Now answer the following questions :
Compare the final electrostatic energy stored in shell A with that in shell B.
As electrostatic energy stored u=12CV2
⇒uAuB=C1V2C2V2=C1C2=R1R2
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - MULTIPLE CHOICE QUESTIONS
35 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - FILL IN THE BLANKS
18 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ADDITIONAL EXERCISES
36 Videos
- ELECTROMAGNETICE INDUCTIONBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Self Assessment Test Section -D
1 Video
- EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D
6 Videos
Similar Questions
A hollow metallic sphere of radius 5 cm is charged so that the potential on its surface is 10 V. Thepotential at the centre of the sphere is
View SolutionA small sphere A of radius r and carrying a charge q is enclosed by a concentric spherical shell B of radius 2r carrying a charge 29. When A and B are connected by a conducting wire, the charge will flow from __________ to __________ .
View SolutionA charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of −2×10−9C from a point P(0,0,3 cm) to a point Q10,4 cm, 0) via a point R(0,6 cm, 9 cm).
View Solution(a) Derive the expression for the magnetic energy stored in an inductor when a current I develops in it. Hence, obtain the expression for the magnetic energy density.
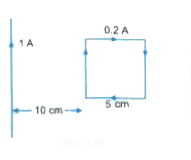
(b) A square loop of sides 5 cm carrying a current of 0.2 A in the clockwise direction is placed at a distance of 10 cm from an infinitely long wire carrying a current of 1 A as shown in Fig. 6.66. Calculate (i) the resultant magnetic force, and (ii) the torque, if any, acting on the loop.
View Solution(a) An electric dipole of dipole moment →p is placed in a uniform electric field →E at an angle θ with it. Derive the expression for torque (→τ) acting on it. Find the orientation of the dipole relative to the electric field for which torque on it is (i) maximum, and (ii) half of maximum.
(b) Two point charges q1=+1μC and q2=+4μC are placed 2 m apart in air. At what distance from q1 along the line joining the two charges, will the net electric field be zero ?
View SolutionThree conducting spherical shells have radii (a, b, and c) such that a<b<c (Fig. 3.113). Initially, the inner shell is uncharged, the middle shell has a positive charge Q, and the outer shell has a negative charge −Q.
 .
.
a. Find the electric potential of the three shells.
b. If the inner and outer shells are now connected by a wire that is insulated as it passes through the middle shell, what is the electric potential of each of the three shells ? Also, what is the final charge on each shell ?
View SolutionShown in the figure a spherical shell with an inner radius 'a' and an outer radius 'b' is made of conducting metarial. A charge +Q is placed at the centre of the spherical shell and a total charge -q s placed on the shell. Charge -q is districuted on the surfaces as :

View SolutionWhen two concentric shells are connected by a thin conducting wire, whole of the charge of inner shell transfers to the outer shell and potential difference between them becomes zero. Surface charge densities of two thin concentric spherical shells are sigma and -sigma respectively. Their radii are R and 2R . Now they are connected by a thin wire. Suppose electric field at a distance r (gt 2R) was E_(1) before connecting the two shells and E_(2) after connecting the two shells, then |E_(2)/E_(1)| is :-
View SolutionWhen two concentric shells are connected by a thin conducting wire, whole of the charge of inner shell transfers to the outer shell and potential difference between them becomes zero. Surface charge densities of two thin concentric spherical shells are σ and −σ respectively. Their radii are R and 2R. Now they are connected by a thin wire.

Suppose electric field at a distance r=3R2 was E1 before connecting the two shells and E2 after connecting the two shells, then ∣∣∣E2E1∣∣∣ is :-
View SolutionAssertion : Spherical shell a in the shown figure has a charge -q and shell B has charge +q . When these two are connected by a thin conducting wire, then whole of the electrostatic potential energy stored between the shell is lost. Reason : Whole of the inner charge will transfer to outer shell B.
View SolutionTwo concentric spherical conducting shells of radii r and R (r<R) carry charges q and Q respectively . The two shells are now connected by a conducting wire. The final charge on the inner shell is
View SolutionSee the figure here. We have two hollow thin spherical shells A and B of radii R, and R, respectively. Initially as shown in Fig. (i) shell B has a charge + Q which is uniformly distributed over its outer surface but shell B has no charge. At a particular instant the two spherical shells are connected by a thin copper wire as shown in Fig. (ii). After a couple of minutes two spherical shells A and B are disconnected again as shown in Fig. (iii).

Now answer the following questions :
What is the ratio of capacitances of shell A and shell B ?
View SolutionSee the figure here. We have two hollow thin spherical shells A and B of radii R, and R, respectively. Initially as shown in Fig. (i) shell B has a charge + Q which is uniformly distributed over its outer surface but shell B has no charge. At a particular instant the two spherical shells are connected by a thin copper wire as shown in Fig. (ii). After a couple of minutes two spherical shells A and B are disconnected again as shown in Fig. (iii).

Now answer the following questions :
What is the ratio of final electric potentials of shell A and shell B ?
View SolutionSee the figure here. We have two hollow thin spherical shells A and B of radii R, and R, respectively. Initially as shown in Fig. (i) shell B has a charge + Q which is uniformly distributed over its outer surface but shell B has no charge. At a particular instant the two spherical shells are connected by a thin copper wire as shown in Fig. (ii). After a couple of minutes two spherical shells A and B are disconnected again as shown in Fig. (iii). Now answer the following questions : Find the ratio of surface charge densities of shell A and shell B.
View SolutionSee the figure here. We have two hollow thin spherical shells A and B of radii R, and R, respectively. Initially as shown in Fig. (i) shell B has a charge + Q which is uniformly distributed over its outer surface but shell B has no charge. At a particular instant the two spherical shells are connected by a thin copper wire as shown in Fig. (ii). After a couple of minutes two spherical shells A and B are disconnected again as shown in Fig. (iii).

Now answer the following questions :
Find the ratio of electric field on the surfaces of shell A and B.
View Solution

