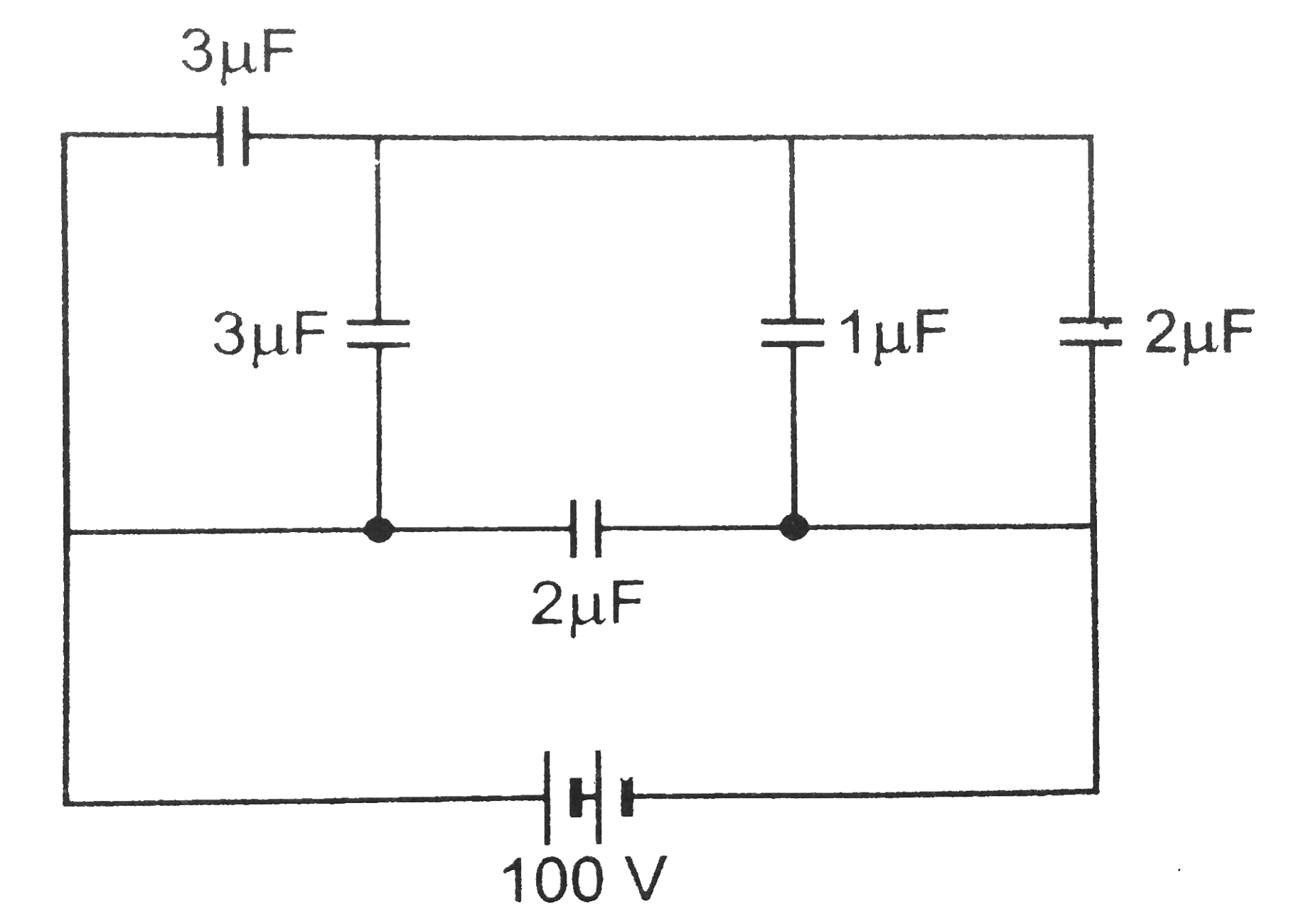
The figure shows a network of five capacitors connected to a 100 V supply, Calculate the total energy stored in the network.
Text Solution
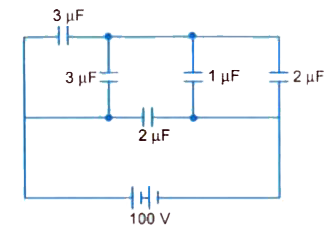
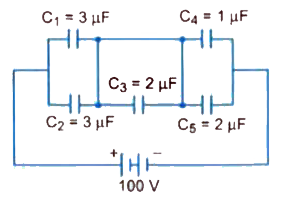
The network of capacitors can be redrawn as shown here. Obviously capacitor C3of2μF is short circuited and is useless.
Capacitance C12 of parallel grouping of C4andC2 is
C12=C1+C2=3+3=6μF
Capacitance C45 of parallel grouping C4andC5 is
C45=C4+C5=3+3=6μF
In the network C12andC45 are in series. So the net capacitance of the arrangement
C=C12×C45(C12+C45)=6×3(6×3)=μF=2μF
∴ Total energy stored int he network
u=12CV2=12×(2μF)×(100V)2
=12×2×10−6×(100)2=10−2J=0.01J
|
Similar Questions
Knowledge Check
A 16 pF capacitor is connected to 70 V supply. The amount of electric energy stored in the capacitor is
A4.5×10−12JB5.1×10−8JC2.5×10−12JD3.92×10−8JIf n capacitors are connected in parallel to a V volt source then total energy of the system is:
ACVB12CV2C12nCV2D12nCV2Figure shows five capacitors connected across a 12V power supply. What is the charge on the 2μF capacitor ?
 A6μCB8μCC10μCD12μC
A6μCB8μCC10μCD12μC
A 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor ?
View SolutionA 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor ?
View SolutionA 600pF capacitor is charged with 100 V battery . Calculate the energy stored and charge on the capacitor .
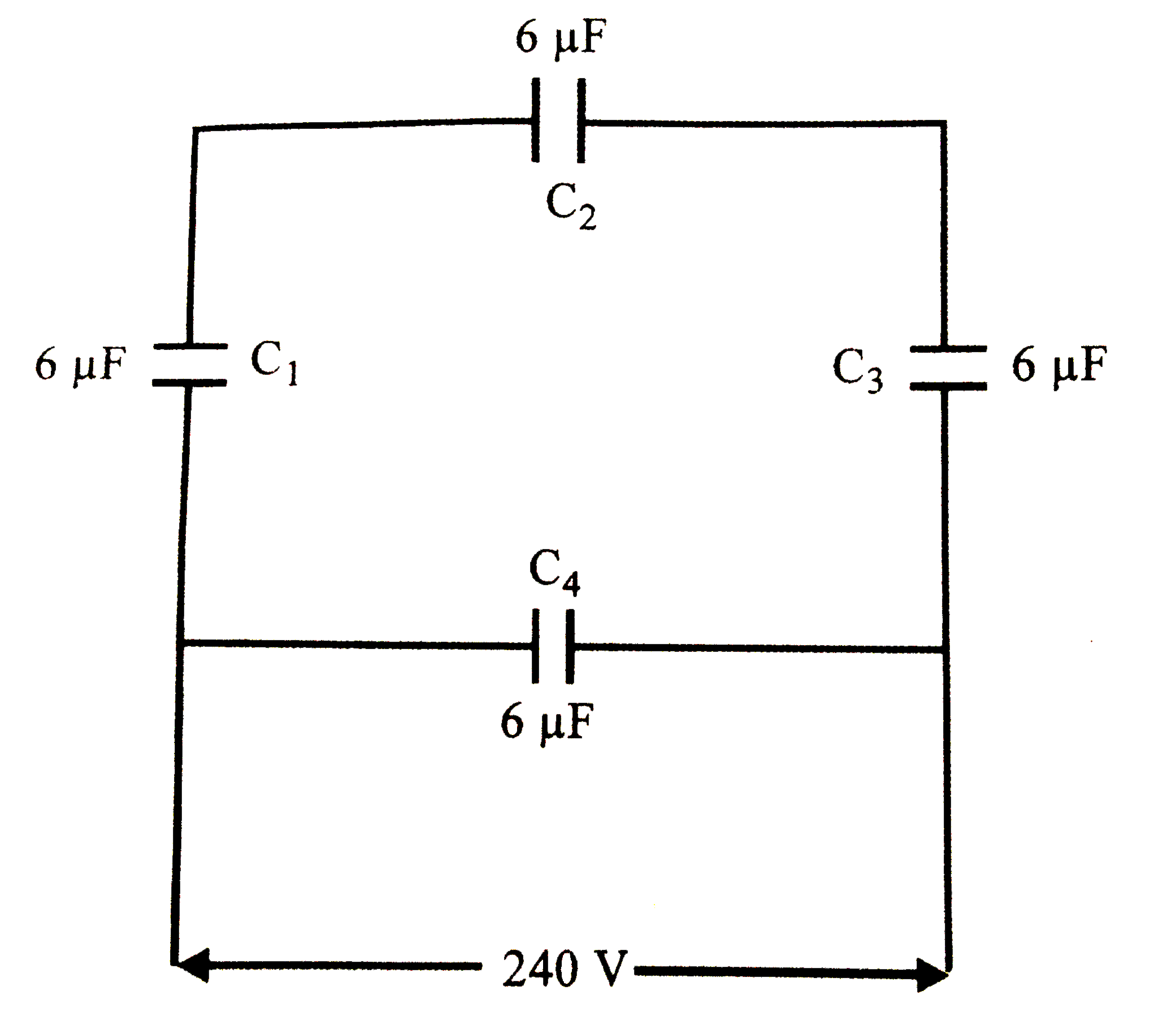
View SolutionA network of four capacitors of 6 μF each is connected to a 240 V supply. Determine the charge on each capacitor.
View SolutionIf there are n capacitors in parallel connected to V volt source, then the energy stored is equal to
View Solution