Establish a relation for electric potential due to short dipole at a point distance r from the dipole along a line inclined at an angle θ from the dipole axis . Hence obtain value of electric potential at a point lying along (i) axial line , (ii) equatoral line of the dipole .
Consider a short electric dipole AB consisting of two charges of −q and +q separated by a small distance AB = 2a . The dipole has a dipole moment →p whose magnitude is q (2a) and which points along AB .
Let P be a point at a distance r from mid-point O of electric dipole and line OP subtends an angle θ from the dipole axis . Then electric potential at point P is given by
V=VA+VB=q4π∈0(AP)+q4π∈0(BP)
Draw normals BC and AD from points B and A respectively on extended line PO. As dipole is a short dipole , hence as shown in fig.
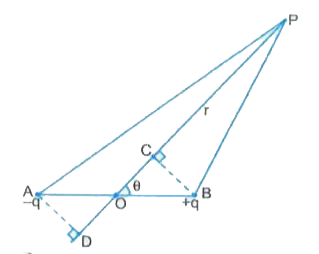
BP=CP=OP−OC=r−acosθ and AP=DP=OP+OD=r+acosθ
∴V=q4π∈0(r+acosθ)+q4π∈0(r−acosθ)=q4π∈0[1(r−acosθ)−1(r+acosθ)]
=q4π∈02acosθ(r2−a2cos2θ)=pcosθ4π∈0(r2−a2cos2θ)=→p⋅→r4π∈0(r2−a2cos2θ)
As a<<r hence the term a2cos2θ may be neglected as compared to r2 and so we have V=pcosθ4π∈0⋅r2=→p⋅→r4π∈0r2
Important cases to be remembered are
(i) If point P lies along axial line of dipole towards +q charge , then θ=0∘ and hence V=p4π∈0⋅r2
(ii) If point P lies along axial line of dipole towards −q charge , then θ=180∘ and hence V=p4π∈0r2
(iii) If point P lies along equatoral line of dipole then θ=90∘ and hence V = 0
Similar Questions
Knowledge Check
The electric potential at a point on the equatorial line of a electric dipole is
Adirectly proportional to the square of the distanceBindirectly proportional to the square of the distanceCdirectly proportional to the chargeDnone of the aboveThe electric field at a point due to an electric dipole, on an axis inclined at an angle θ(<90∘) to the dipole axis, is perpendicular to the dipole axis, if the angle θ is
Atan−1(2)Btan−1(12)Ctan−1(√2)Dtan−1(1√2)If Ea be the electric field of a short dipole at a point on its axial line and Ee that on the equatorial line at the same distance ,then
AEa=2EeBEe=2EaCEa=EeDnone of these
Derive an expression for the electric potential at any point along the axial line of an electric dipole.
View SolutionThe electric potential at a point distant 0.1m from the middle of a short electric dipole on a line inclined at an angle of 60∘ with the dipole axis is 900V. Calculate the dipole moment.
View SolutionThe electric field at a point due to an electric dipole, on an axis inclined at an angle θ(<90∘) to the dipole axis, is perpendicular to the dipole axis, if the angle θ is
View SolutionDerive an expression for the electric field at any point along the axial line of an electrical dipole.
View SolutionA short electric dipole has dipole moment of 4×10−9Cm. Determine the electric potential due to the dipole at a point distant 0.3 m from the centre of the dipole situated on (a) the axial line (b) on equatorial line and (c) on a line making an angle of 60∘ wth the dipole axis.
View Solution

