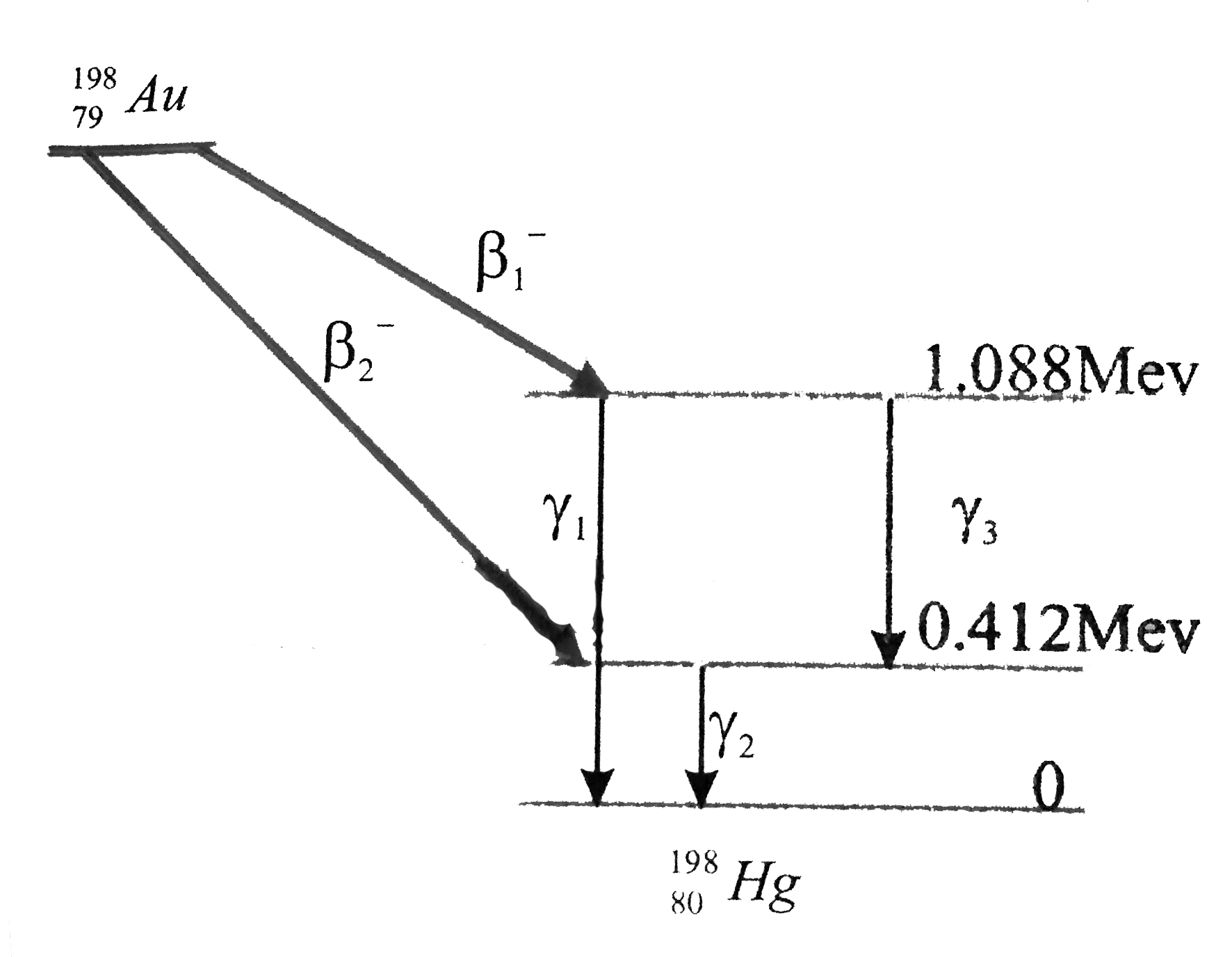
Obtain the maximum kinetic energy of B-particles, and the radiation frequencies of y decays in the decay scheme shown in Fig.13.01. You are given that

m(198Au)=197.968233u and m(198Hg)=197.966760u
Frequency corresponding to γ-decay ν=E2−E1h
∴ν(γ1)=(1.088−0)×1.6×10−136.626×10−34=2.627×1020Hz
ν(γ2)=(0.412−0)×1.6×10−136.626×10−34=9.950×1019Hz
and ν(γ3)=(1.088−0.412)×16×10−136.626×10−34=1.632×1020Hz
β−2-decay can be represented by 19879Au→ 19880Hg+ 0−1e+Q(β−1)+Q(γ1), where Q(γ1)=1.088MeV
Maximum kinetic energy of β−1 particles is
EKmax(β−1)=[m( 19879Au)−m( 19880Hg)]931.5MeV−1.088MeV=(197.968233—197.966760)×931.5MeV−1.088MeV=0.284MeV
β−2-decay can be represented by 19879Au→ 19880Hg+ 0−1e+Q(β−2)+Q(γ2), where Q(γ2)=0.412MeV
Maximum kinetic energy of β−2 is EKmax(β−2)=(197.968233−197.966760)×931.5MeV−0.412MeV=0.960MeV.
Topper's Solved these Questions
- NUCLEIBOOK - U-LIKE SERIESCHAPTER - NUCLEIEXERCISE - CBSE Based/Source -Based Integrated Questions
3 Videos
- NUCLEIBOOK - U-LIKE SERIESCHAPTER - NUCLEIEXERCISE - Multiple Choice Questions
30 Videos
- NUCLEIBOOK - U-LIKE SERIESCHAPTER - NUCLEIEXERCISE - Self Assessment Test
10 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - SELF ASSESSMENT TEST (SECTION D)
1 Video
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - U-LIKE SERIESCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - SELF ASSESSMENT TEST (SECTION B)
3 Videos
Similar Questions
Read the following passage and then answer questions (a) - (e) on the basis of your understanding of the passage and the related studied concepts.
Rutherford was the pioneer who established the existence of the atomic nucleus. Result of Geiger and Marsden experiment on the scattering of a-particles from thin gold foils, performed at Rutherford’s suggestion, revealed that the distance of closest approach to a gold nucleus of an a-particle of kinetic energy 5.5 MeV is about 4.0×10−14m. The said scattering effect was explained by Rutherford by assuming that the Coulombian repulsive force was solely responsible for scattering. Since the positive charge is confined to the nucleus, the actual size of the nucleus has to be less than 4.0×10−14m.
If we use a-particles of higher energies, the distance of closest approach to the gold nucleus will be still smaller. At some point the scattering will begin to be affected by the short range nuclear forces and differ from Rutherford’s calculations. From the distance at which deviations set it, nuclear size can be inferred.
(a) Define MeV and express its value in terms of SI unit of energy.
(b) What is distance of closest approach ?
(c) Write an expression for distance of closest approach of a-particle to a gold nucleus.
(d) What was Rutherford’s hypothesis regarding the existence of the atomic nucleus ?
(e) How can you show that volume of the nucleus of an element is proportional to its mass number ?
View SolutionOrder of magnitude of density of uranium nucleus is
View SolutionThe binding energy of 21H is 1.112 MeV per nucleon and an alpha-particle 42He has a binding energy of 7.047 MeV per nucleon. In the fusion reaction 21H+ 21H→ 42He+Q, the energy released is
View Solution(a) Derive the expression for the magnetic field due to a current carrying coil of radius r at a distance x from the centre along the X-axis.
(b) A straight wire carrying a current of 5 A is bent into a semicular arc of radius 2 cm as shown in the fig. FInd th magnitude and direction of the magnetic field at the centre of the arc.

View SolutionA beam of light converges at aoint P. Now a convex lens is placed in the path of the convergent beam at 15 cm from P. At what point does a beam converge if the convex lens has a focal length 10 cm?
View SolutionConsider the beta decay
^198Au→198Hg∗+Bη−1+→v.
where ^198Hg∗ represents a mercury nucleus in an excited state at energy 1.088MeV above the ground state. What can be the maximum kinetic energy of the electron emitted? The atomic mass of ^198Au is 197.968233u and that of ^198Hg is 197.966760u.
View SolutionThe half-life of ^198Au is 2.7days. Calculate (a) the decay constant, (b) the average-life and (C ) the activity of 1.00mg of ^198Au. Take atomic weight of ^198Au to be 198gmol−1.
View SolutionGold ._(79)^(198)Au undergoes beta^(-) decay to an excited state of ._(80)^(198)Hg . If the excited state decays by emission of a gamma -photon with energy 0.412 MeV , the maximum kinetic energy of the electron emitted in the decay is (This maximum occurs when the antineutrino has negligble energy. The recoil enregy of the ._(80)^(198)Hg nucleus can be ignored. The masses of the neutral atoms in their ground states are 197.968255 u for ._(79)^(198)Hg ).
View SolutionObtain the maximum kinetic energy of β-particles, and the radiation frequencies of γ decays in the decay scheme shown in Fig. 14.6. You are given that m(.198Au)=197.968233u,m(.198Hg)=197.966760u
View Solutionनीचे दी गई क्षय योजना में γ क्षयों की विकिरण आवृत्तियां एवं β कणों की अधिकतम गतिज ऊर्जाएं ज्ञात कीजिए। दिया है
m(.198Au)=197.968233u
m(.198Hg)=197.966760u

View Solutionनीचे दी गयी क्षय योजना ( decay scheme ) में β - कणो की अधिकतम गतिज उर्जाएँ था γ - कानो की विकिरण आवृत्तियाँ (radiation frequencies ) ज्ञात करे |

दिया गया है :m(19879Au)=197.968233 u
m(19880Hg)=197.966760u .
View SolutionObtain the maximum kinetic energy of β- particle and the radiation frequencies corresponding to γ− decays in the figure given below. (rest mass of au -198.968233 u and r.m. of Hg=198=197.966760 u)
View Solution198Au की अर्ध - आयु 2.7 दिन है | 1.0mg198Au का (a) क्षय स्थिरांक , (b) औसत आयु और (c) सक्रियता निकालें
View SolutionObtain the maximum kinetic energy of b-particles, and the radiation frequencies of g decays in the decay scheme shown in Fig. You are given that m(""_(8)^(19)Au) = 197.968233 u m(""_(8)^(19)Hg) =197.966760 u .
View SolutionGold nucleus (""_(79)^(198)Au) can decay into mercuyr nucleus (""_(80)^(198)Hg^(8)) by two decay schemes shown in figure below (i) it can emit a beta -particle (beta_(1)) and come to ground state by either emiting one gamma - ray ( gamma_(1) ) or emitting two gamma - rays ( gamma_(3) and gamma_(4) ) (ii) It can emit one beta - particle (beta_(2)) and come to ground state by emitting gamma_(2) ray. Atomic masses: ""^(198)Au=197.9652 amu and ""^(198)Hg=197.9662 amu. Given that 1 amu= 930MeV//c^(2) . The energy levels of the nucleus are shown in figure below Whatis the maximum kinetic energy of emitted beta_(2) particle?
View SolutionGold nucleus (19879Au) can decay into mercuyr nucleus (19880Hg8) by two decay schemes shown in figure below (i) it can emit a β -particle (β1) and come to ground state by either emiting one γ- ray (γ1) or emitting two γ- rays (γ3 and γ4) (ii) It can emit one β- particle (β2) and come to ground state by emitting γ2 ray. Atomic masses: 198Au=197.9652 amu and 198Hg=197.9662 amu. Given that 1 amu= 930MeV/c2. The energy levels of the nucleus are shown in figure below
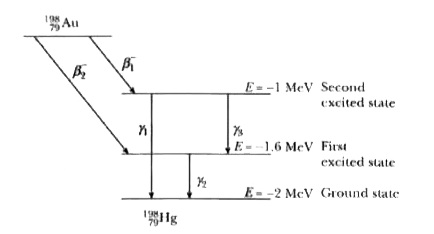
What is the maximum kinetic energy of emitted β1 parricle ?
View Solution

