Obtain the formula for the electric field due to a long thin wire of uniform linear charge density E without using Gauss's law. (Hint: Use Coulomb's law directly and evaluate the necessary integral.)
Solution in Gujrati
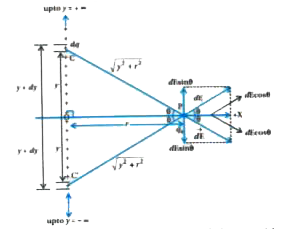
Consider infinitely extended line of charge with constant linear charge density λ . Let us determine its electric field at perpendicular distance r say at point P as shown in the figure. For this consider a charge element dq at distance y from central point O. Here, dq=λdy
(∴λ=dqdy)
Magnitude of Coulombian force exerted by above charge element dq on test charge q0 placed at point P is,
dF=k(dq)q0(CP)2=k(dq)q0y2+r2........(1)
Magnitude of electric field of charge element dq at point P is,
dE=dFq0=kdqy2+r2.........(2)
Similary magnitude of electric field of charge element dq (selected on opposite side of central point O) at point P is also, dE=kdqy2+r2
When we resolve above two electric fields into two mutually perpendicular components at point p we find that dEsinG components cancel each other (because of equal magnitudes and opposite directions). Hence, we get electric field at point P only due to dEcosθ components which are in same directions and so we can make their scalar addition to find resultant electric field E at point P Thus,
E=∫dEcosθ
∫kdqy2+r2.r√y2+r2
From eqn. (2) and from ΔCOP
∴E=∫kλdy×r(y2+r2)3/2...........(3)
In right angled △COP
tanθ=yr⇒y=rtanθ.......(4)
For a given point P value of r is constant and so from above equation,
dydθ=rddθ(tanθ)
∴dydθ=rsec2θ
∴dy=rsec2θdθ........(5)
Now, (y2+r2)3/2=(r2tan2θ+r2)3/2 (From equation (4))
=(r2sec2θ)3/2
=r2sec3θ.........(6)
From equation (4)
tanθ=yr
When y=−∞,tanθ=−∞⇒θ=−π2
y=+∞,tanθ=+∞⇒θ=+π2 ............(7)
From eqn (3), (5),(6) and (7),
E=∫+π/2−π/2kλ(rsec2θdθ)×rr3sec3θ
∴E=kλr{sin(π2)−sin(−π2)}
∴E=2kλr
∴E=λ2πε0r(∴k=14πε0)
Similar Questions
Obtain the formula for the electric field due to a long thin wire of uniform linear charge density E without using gauss law
View SolutionObtain the formula for the electric field due to a long thin wire of uniform linear charge density λ without using Gauss's law. [Hint.use Coulomb's law directly and evaluate the necessary integral ].
View SolutionObtain the formula for the electric field due to a along thin wire of uniform linear charge density λ without using Gauss's law.
View SolutionObtain the formula for the electric field due to a long thin wire of uniform linear charge density E without using gauss law
View SolutionObtain the formula for the electric field due to a long thin wire of uniform linear charge density E without using gauss law
View SolutionObtain the formula for the electric field due to a long thin wire of uniform linear charge density E without using gauss law
View SolutionUsing Gauss’s law, determine the electric field intensity due to a long thin wire of uniform charge density.
View Solution
