Consider A, D and C to be the co-centric shells of metal . Their radii are a ,b and c respectively (a < b < c). Their surface charge densities are σ,−σ and σ respectively. Calculate the electric potential on the surface of shell A.
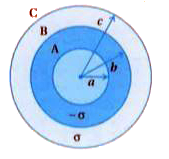 Solution in Gujrati
Solution in Gujrati
σε0[a2−b2a+c]
σε0[a2−b2b+c]
σε0[a2−b2b+a]
σε0[a2−b2c+a]
The correct Answer is:A, B, C
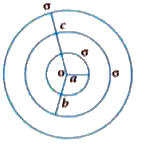
Potential ins.ide the shell and on surface is same
V=kqR
where R is radius of shell and potential at r>R distance V=kqR
Vb=kqab+kqbb+kqcb but q=4pπ2σ
∴Vb=4πa2σ4π∈0×b+4πb2(−σ)4π∈0×b+4π∈2(σ)4π∈0×c
=a2σ∈0b−b2σ∈0b+c2σ∈0c
=σ∈0[a2−b2b+c]
Similar Questions
तीन संकेद्रीय गोलीय कोश की त्रिज्याएँ a, b व c(a<b<c) हैं तथा इनके आवेश पृष्ठ घनत्व क्रमशः σ,−σवσ हैं | यदि VA,VBवVC तीनों गोलीय कोश के विभव हों , तब c = a + b , के लिये है
View SolutionThree concentric spherical metal shells A.B.C of radii a,b,c(c>b>a) have surface charge density +σ,−σand+σ respectively. The potential of the middle shell is σε0 times
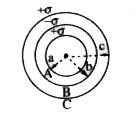
View SolutionThree concentric metallic spherical shell A,B and C or radii a,b and c(a<b<c) have surface charge densities −σ,+σand−σ. Respectively. The potential of shel A is :
View SolutionThree concentric spherical metal shells A, B, C of radii a, b, c (c>b> a) have surface charge density +σ,−σand +σ respectively. The potential of the middle shell is σε0times
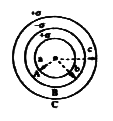
View SolutionThree concetric sphereical metal shells A,B,C or radii a,b,c (c gt b gt a) have surface charge densities +sigma , - sigma and +sigma respectively. (a) Find the potentials of the three shells ? (b) If the shells A and C are at same potential , find the relation between a,b and c.
View SolutionThree concentric metallic spherical shells A,B and C of radii a,b and c(a<b<c) have surface charge densities +σ,−σand +σ respectively ,the potential of shell B is
View SolutionThree concentric spherical metallic shells A, B and C of radii a, b and c (a lt b ltc) have surface charge densities σ, −σ and σ respectively.
(i) Find the potential of the three shells A, B and C.
(ii) If the shells A and C are at the same potential, obtain the relation between the radii a, b and c.
View Solution

