What contradiction is found by using ampere circuital law to obtain magnetic field during charging of capacitor ? Solution in Gujrati
In figure (a) parallel plate capacitor (C ) is shown in its charging state. During charging of capacitor at time t current i(t) flows which is obtained from battery. No current flow inside capacitor.
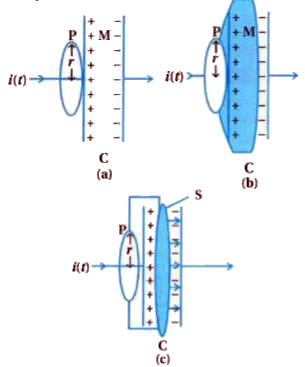
A parallel plate capacitor C, as part of a circuit through which a time dependent current i(t) flows, (a) a loop of radius r, to determine magnetic field at a point P on the loop , (b) a pot - shaped surface passing through the interior between the capacitor plates with the loop shown in (a) as its rim , (c ) a tiffinshaped surface with the circular loop as its rim and a flat circular bottom S between the capacitor plates. the circular bottom S between the capacitor plates. The arrows show uniform electric field between the capacitor plates.
At a point P outside capacitor, consider loop of radius r whose centre is on the wire plane is perpendicular to wire.
From symmetry it can be shown that at any point on the loop magnetic field is along circumference of the loop and magnitude is equal of at any point of the loop.
By using ampere circuital law point P outside capacitor,
∮→B.→dl=μ0i(t) ....(1)
where ΣI=i(t) is total current.
If ∣∣→B∣∣=B and ∮→dl=2πr, then
B(2πr)=μ0i(t) ...(2)
Now consider another surface shown in figure (b) which do not touch current carrying conductor bottom of surface lies in region between plates.
Also in figure (c ) consider oval shaped surface which is between plates of capacitor and radius equal to r. In figure (b) and (c ) current do not flow in closed surface considered hence closed surface having radius r by using ampere circuital law.
In ∫→B.→dl=μ0ΣI
∫dl=2πr
ΣI=μ0i(t)=0
Thus, we get different value of magnetic field outside and inside which is contradictory. Thus, outside and inside which is contradictory. Thus, outside plates of capacitor we get non - zero magnetic field and inside (between) plates of capacitor magnetic field is zero.
This contradiction is by using ampere circuital law hence it can be said that there is something missing in ampere circuital law.
Similar Questions
(A) : The magnetic field at the centre of a circular coil carrying current could be calculated using Amperes circuital law. (R) : Biot savart law could be derived from Amperes law.
View Solution(A) : The magnetic field in the open space inside and exterior to the toroid is zero.
(R) : Field produced by a toroid could be derived using Amperes circuital law.
View SolutionIn an oscillating L-C circuit the maximum charge on the capacitor is Q. What will be the charge on the plate of the capacitor, when energy stored in magnetic field and electric field are equal ?
View SolutionState Ampere's circuital law. Using this law obtain an expression for the intensity of the magnetic field on the axis of a toroidal solenoid for a current of I ampere.
View SolutionState the Ampere’s circuital law Obtain for the magnetic field at the point on axis of a solenoid.
View SolutionQuestions|Magnetic Field Lines|Magnetic Field Lines Due To Important Structure|Ampere Circuital Law
View SolutionAmpere Circuital Law|Magnetic Field Due To Hollow Cylindrical Wire
View SolutionIn an oscillating LC circuit the maximum charge an capacitor is Q The charge on the capacitor when the is stored equally between the electric and magnetic field
View Solution

