In the given figure, O is the centre of a circle. If ∠AOB=100∘ and ∠AOC=90∘ then ∠BAC=?
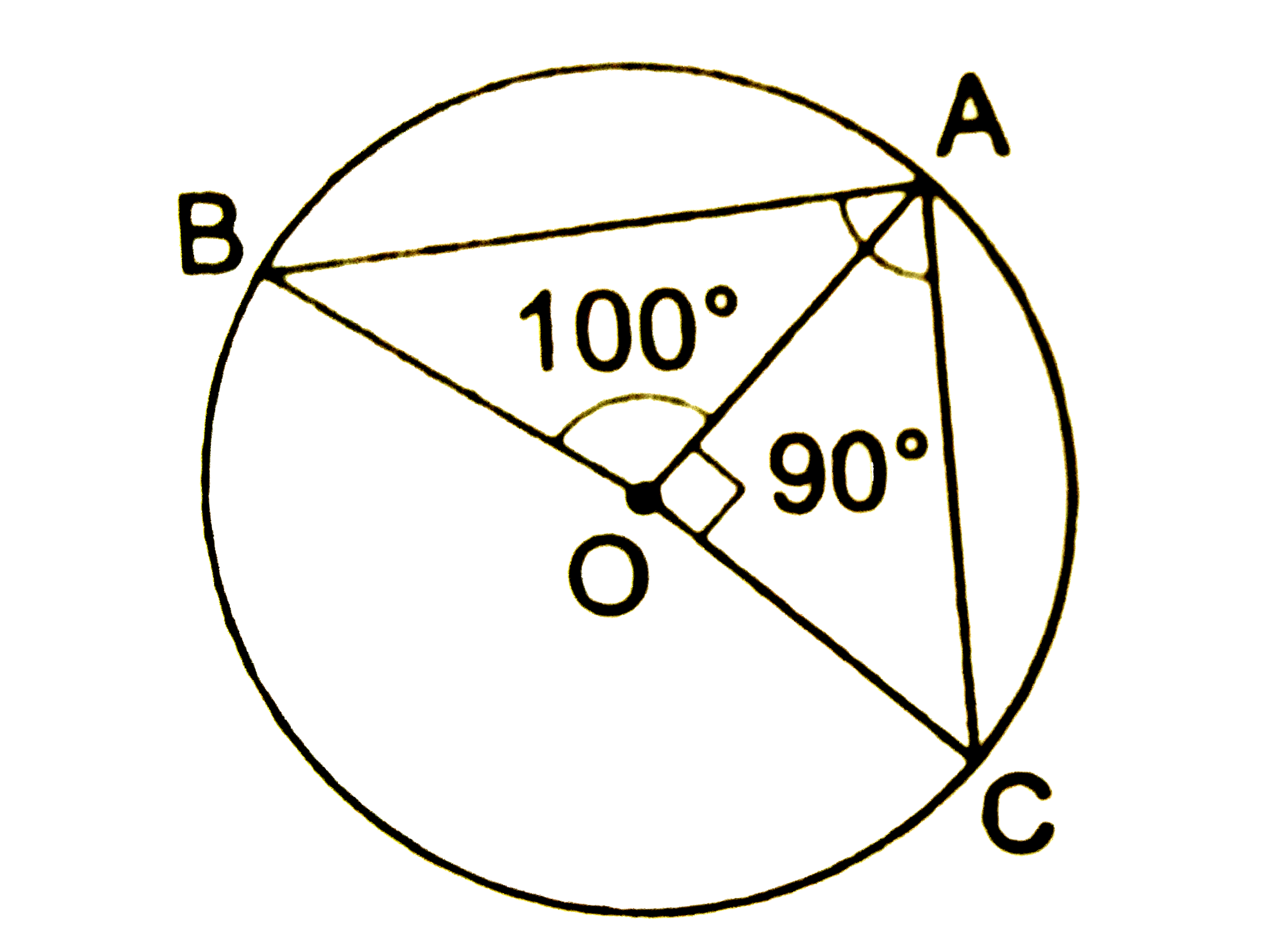
A
85∘
B
80∘
C
95∘
D
75∘
Video Solution
Text Solution
The correct Answer is:A
∠BOC+∠BOA+∠AOC=360∘⇒∠BOC=360∘−190∘=170∘
∴∠BAC=12×170∘=85∘
|
Topper's Solved these Questions
- CIRCLES Book:RS AGGARWALChapter:CIRCLES Exercise:Multiple Choice Questions (Mcq)
Explore 5 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBook:RS AGGARWALChapter:BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONExercise:EXERCISE 17B
Explore 16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Multiple Choice Questions (Mcq)
Explore 20 Videos
Similar Questions
Knowledge Check
In the given figure, , O is the centre of a circle and ∠AOB=140∘. Then , ∠ACB=?
 A70∘B80∘C110∘D40∘
A70∘B80∘C110∘D40∘In the given figure, O is the centre of circle, ∠AOB=100∘. Find ∠BCD :
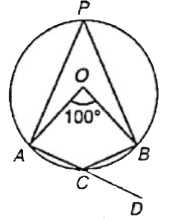 A80∘B60∘C50∘D40∘
A80∘B60∘C50∘D40∘In the given figure, O is the centre of the circle. The value of x is
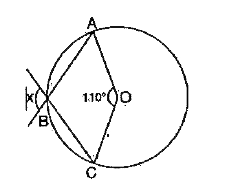 A75∘B55∘C125∘D110∘
A75∘B55∘C125∘D110∘
In the given figure,O is the centre of the circle ∠OAB=30∘ and ∠OCB=40∘. Calculate ∠AOC
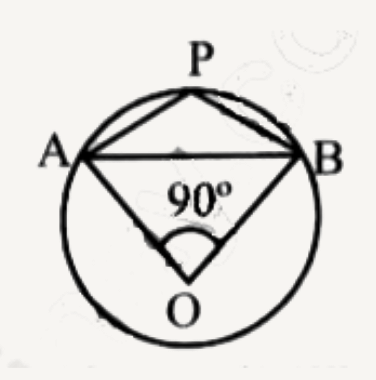
View SolutionIn the given figure, O is the centre of the circle, ∠AOB=90∘. Find ∠APB :
View SolutionIn Figure, O is the centre of the circle. If ∠APB=500, find ∠AOB and ∠OAB
View SolutionIn the given figure, O is the centre of the circle∠AOB=90∘ Find m∠APB
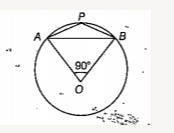
View SolutionIn Fig, O is the center of the circle. Find the angle of △ABC.

View Solution