In the adjoining figure, the bisectors of ∠Band∠D of a quadrilateral ABCD meet CD and AB produced at P and Q respectively.
Proove that
∠P+∠Q=12(∠B+∠D).
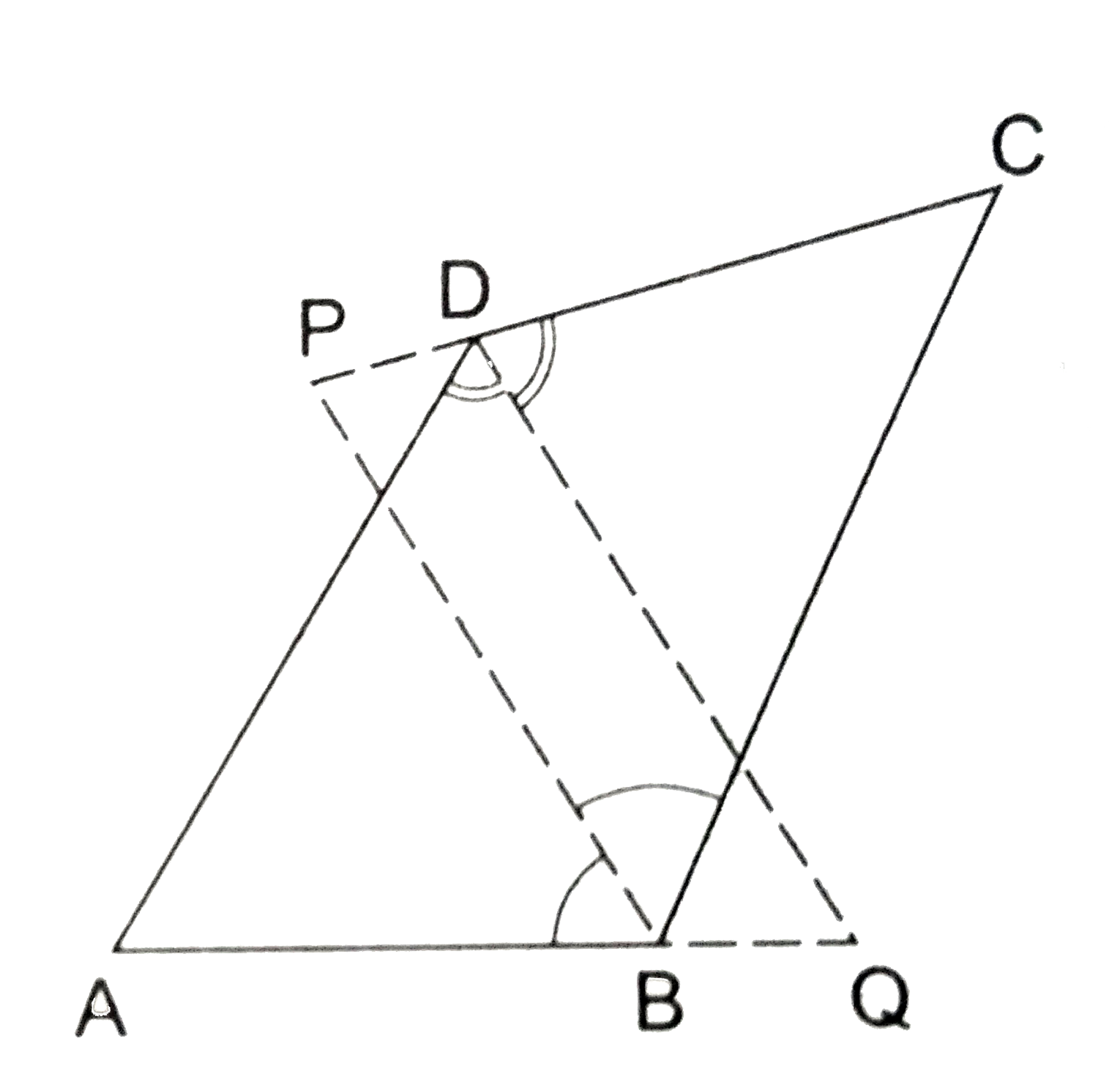
In ∠ADQ, we have
∠A+∠ADQ+∠Q=180∘(sum of the ∠ of a △)
⇒∠A+12∠D+∠Q=180∘. …(i)
In △CBP, we have
∠C+∠CBP+∠P=180∘(sum of the ∠ of a △)
⇒∠C+12∠B+∠P=180∘. ...(ii)
Adding (i) and (ii), we get
∠A+∠C+12∠B+12∠D+∠P+∠Q=360∘
⇒∠A+∠C+∠B+∠D+∠P+∠Q=360∘+12∠B+12∠D [ adding (12∠B+12∠D) on both sides]
⇒360∘+∠P+∠Q=360∘+12(∠B+∠D) [∵ sum of all the angles of a quardrilateral is 360∘]
⇒∠P+∠Q=12(∠B+∠D).
Similar Questions
In the given figure, the angles ∠ADE and ∠ABC differ by 15∘. Find ∠CAE.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E06_005_Q01.png" width="80%"gt
View SolutionIf bisectors of ∠Aand∠B of a quadrilateral ABCD intersect each other at P, of ∠Band∠C at Q, of ∠Cand∠D at R and of ∠Dand∠A at S then PQRS is a
View SolutionABCDE is a regular pentagon. Angle bisector of ∠BAE meets CD at m. angle bisector of ∠BCD meets AM at P. Find the ∠CPM= ?
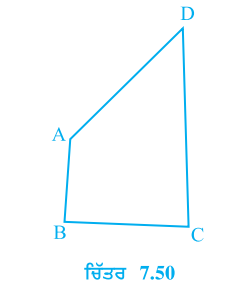
View SolutionAB ਅਤੇ CD ਕ੍ਰਮਵਾਰ ਇੱਕ ਚਤੁਰਭੁਜ ABCD ਦੀ ਸਭ ਤੋਂ ਛੋਟੀ ਅਤੇ ਸਭ ਤੋਂ ਵੱਡੀ ਭੁਜਾ ਹੈ (ਦੇਖੋ ਚਿੱਤਰ 7.50)। ਦਿਖਾਓ ਕਿ ∠A>∠C ਅਤੇ ∠B>∠D ਹੈ।
View SolutionIn the following figure , angle B=90∘∠ADB=30∘and∠ACB=60∘
If ∠CD=m find AB .
(##SEL_RKB_ICSE_MAT_IX_CR_02_E01_162_Q01.png" width="80%">
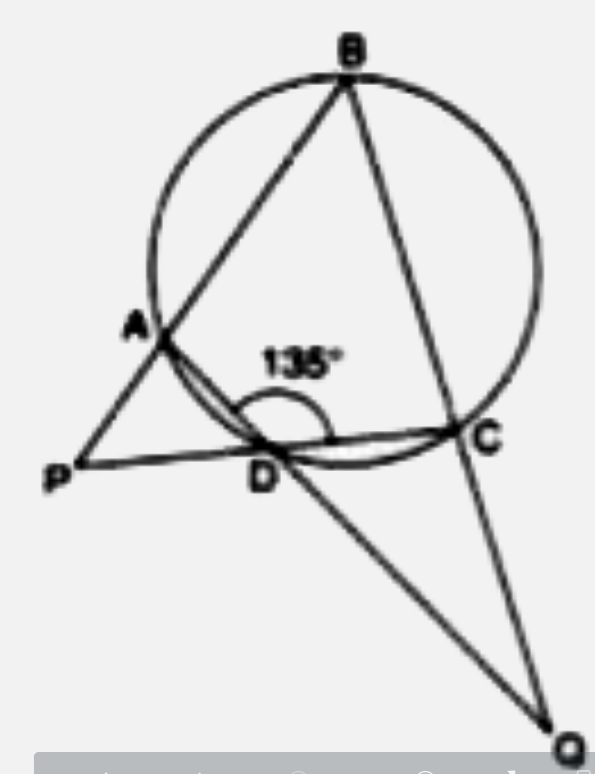
View SolutionABCD is a syclic quadrilateral with ∠ADC=135∘. Sides BA and CD produced meet at point P, sides AD and BC produced meet at point Q.If∠P:∠Q=2:1, find angles P and Q.
View SolutionIn the figure of a quadrilateral ABCD angleB And angleD The angle bisectors of the lines CD and AB meet at P and Q respectively, then angleP And angleQ And angleABC And angleADC What will be the relation in
View SolutionIdentify A,B,C and D,E
View Solution