Two concentric circles of radii a and b(a>b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
2√a2+b2
2√b2−a2
2√a2−b2
none of these
The correct Answer is:C
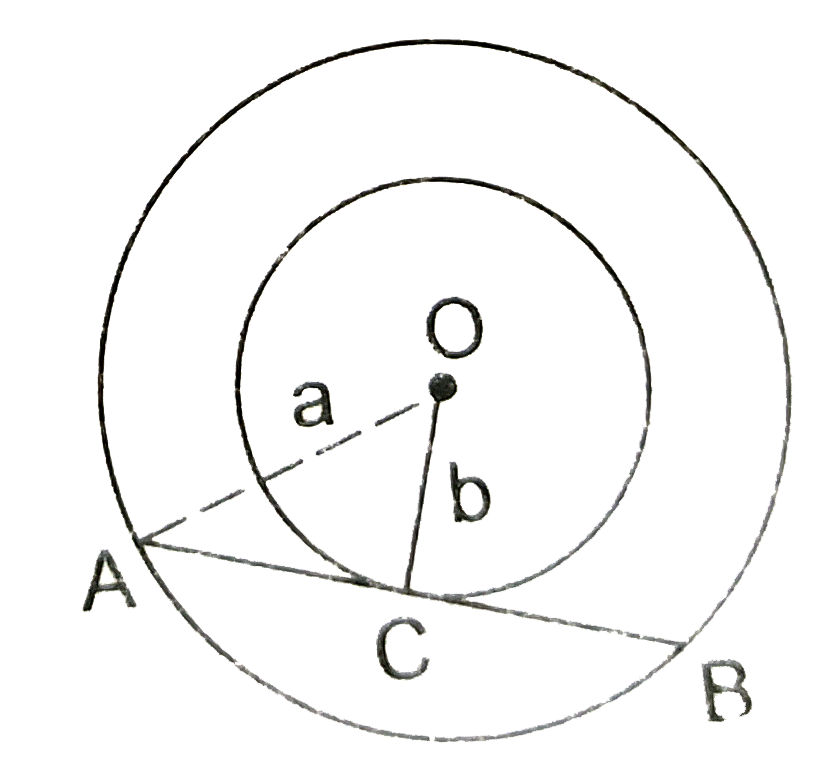
Let O be the comon centre of the two circles and AB be the chord of the larger circle which touches the samller circle at C. Join OA and OC. Then, OA=a and OC=b .
Now, OC⊥AB and OC bisects AB [∵ the chord of the larger circle touching the smaller circle, is bisected at the point of contact]
In right, ΔACO, we have
OA2=OC2+AC2[ by Pythagoras' theorem]
⇒AC=√OA2−OC2=√a2−b2.
∴AB=2AC=2√a2−b2 [∵C is the midpoint of AB]
i.e., required length of the chord AB=2√a2−b2.
Similar Questions
Two concentric circles are of radii 5cm and 3cm respectively. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionType III: Two concentric circles of radii 5cm and 3cm . Find the length of the chord of the larger circle which touches the smaller circle.
View Solution
Knowledge Check
Two concentric circles are of radii 13 cm and 5 cm. The length of the chord of the larger circle which touches the smaller circle is:
दो संकेंद्री वृत्तों की त्रिज्या 13 सेमी तथा 5 सेमी है। बड़े वृत्त की जीवा की लंबाई ज्ञात कीजिए, जो छोटे वृत्त को स्पर्श करती है।A6 cmB7 cmC10 cmD8 cm
Two concentric circles are of radii 6.5cm and 2.5cm. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionTwo concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionTwo concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionTwo concentric circles are of radii 5 cm. and 3 c. Find the length of the chord of the larger circle which touches the cmaller circle.
View SolutionTwo concentric circles are of radii 13 cm and 5 cm. Find the length of the chord of the larger circle which touches the inner circle.
View SolutionTwo concentric circles are of diameters 30cm and 18cm. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionTwo concentric circles are of diameter 30 cm and 18 cm. Find the length of the chord of the larger circle which touches the smaller circle.
View Solution