A circle is inscribed in a ΔABC, touching AB, BC and AC at P, Q and R respectively. If AB=10cm, AR=7cm and CR=5cm, find the length of BC.
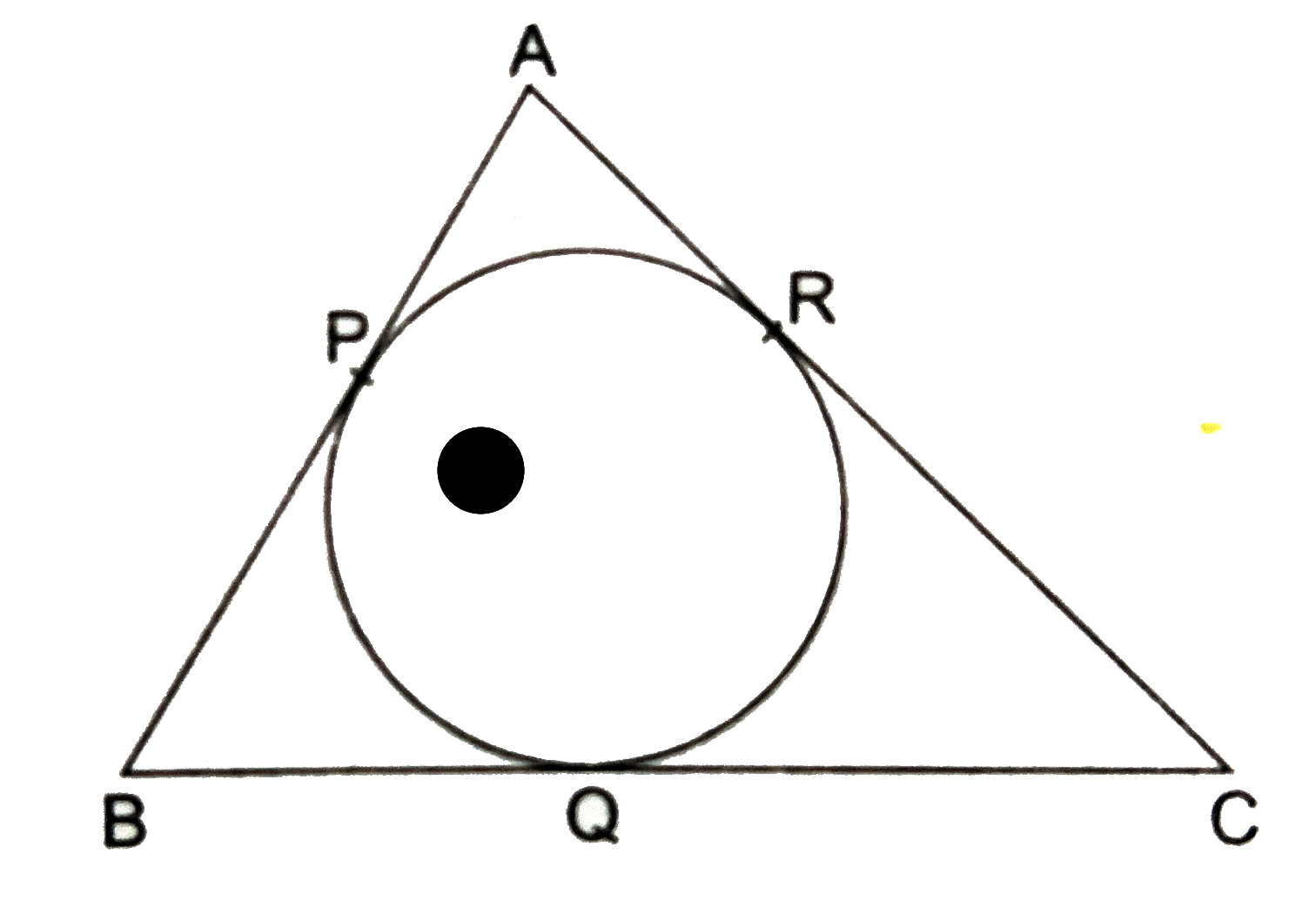
We knoe that the tangents to a circle from an exterior point are equal.
∴AP=AR=7cm,
BQ=BP=AB−AP=(10−7)cm=3cm,
CQ=CR=5cm.
And so, BC=BQ+CQ=(3+5)cm=8cm.

Similar Questions
A circle is inscribed in a ΔABC touching AB, BC and AC at P, Q and R respectively. If AB = 10 cm, AR = 7 cm and CR = 5 cm, then find the length of BC.
View SolutionIn the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F respectively. If AB= 12 cm, BC= 8 cm and AC = 10 cm, find the lengths of AD, BE and CF.
View Solution
Knowledge Check
The sides AB, BC and AC of a ΔABC are 12 cm, 8 cm and 10 cm respectively. A circle is inscribed in the triangle touching AB, BC and AC at D, E and F, respectively. The difference between the lengths of AD and CE is:
Aa)4 cmBb)5 cmCc)3 cmDd)2cm
A circle is inscribed in △ABC, touching AB, BC and AC at points P, Q and R respectively. If AB-BC = 4cm, AB-AC = 2cm and the perimeter of △ABC=32cm, then PB+AR is equal to :
/ एक वृत्त त्रिभुज ABC के भीतर स्थित है जो AB, BC और AC को क्रमशः बिंदु P, Q और R पर स्पर्श करता है | यदि AB-BC =4 सेमी, AB-AC =2 सेमी और त्रिभुज ABC का परिमाप = 32 सेमी है, तो PB+AR का मान ज्ञात करें
View SolutionA circle is inscribed in a triangle ABC. It touches sides AB, BC and AC at point P, Q and R respectively. If BP=9cm, CQ=10cm and AR=11cm, then the perimeter (in cm) of the triangle △ABC is:
त्रिभुज ABC के अंदर एक वृत्त बनाया गया है| यह AB, BC और ACभुजाओं को क्रमशः P, Q और R बिंदुओं पर स्पर्श करता है। अगर BP=9cm, CQ=10cm और AR=11cm है तो △ABC की परिमिति (cm में) हैः
View SolutionA circle is inscribed in a triangle ABC. It touches sides AB, BC and AC at the points P, Q and R respectively. If BP=8.5cm, CQ= 6.5cm and AR=4.5cm,then the perimeter (in cm) of the △ABC is:
त्रिभुज ABC के अंदर एक वृत्त बनाया गया है| यह AB, BC और AC भजाओुं को क्रमशः P, Q और R बिंदुओं पर स्पशे करता है| अगर BP=8.5cm, CQ= 6.5cm और AR=4.5cm है, तो △ABC की परिमिति (cm में) हैः
View SolutionA circle is inscribed in a triangle ABC. It touches sides AB, BC and AC at points P, Q and R respectively. If BP = 5cm, CQ = 7 cm and AR = 6 cm, then the perimeter (in cm) of the is △ABC is:
एक वृत्त किसी त्रिभुज ABC के भीतर स्थित है | यह भुजाओं AB, BC और AC को क्रमशः P, Q और R पर स्पर्श करता है | यदि BP = 5 सेमी, CQ = 7 सेमी और AR = 6 सेमी है, तो त्रिभुज ABC का परिमाप ( सेमी में ) ज्ञात करें |
View SolutionA circle is inscribed in a quadrilateral ABCD , touching sides AB , BC , CD and DA at P , Q , R , and S respectively. If AS = 8 cm , BC = 11 cm and CR = 5 cm, then the length AB is equal to :
एक वृत्त किसी चतुर्भुज ABCD के भीतर स्थित है जो भुजा AB, BC, CD तथा DA को क्रमशः P, Q, R और S पर स्पर्श करता है | यदि AS = 8 सेमी, BC = 11 सेमी और CR =5 सेमी है, तो AB की लंबाई ज्ञात करें |
View SolutionA circle is inscribed in a triangle ABC. It touches sides AB, BC and AC at points P, Q and R respectively. If BP = 5.4 cm, CQ = 7.3 cm and AR = 6.1 cm, then the perimeter (in cm) of the triangle ABC is :
एक वृत्त किसी त्रिभुज ABC के भीतर स्थित है | यह भुजाओं AB, BC और AC को क्रमशः बिंदु P, Q और R पर स्पर्श करता है | यदि BP = 5.4 सेमी, CQ = 7.3 सेमी और AR =6.1 सेमी है, तो त्रिभुज ABC का परिमाप ( सेमी में) ज्ञात करें |
View SolutionA circle is inscribed in a triangle ABC, It touches side AB, BC and AC at points R, P and Q, respectively. If AQ= 3.5cm, PC = 4.5cm and BR = 7cm, then the perimeter (in cm) of the triangle ABC is:
एक वृत्त, त्रिभुज ABC में अन्तर्निहित है, यह क्रमशः AB, BC और AC को R, P और Q के बिंदुओं पर स्पर्श करता है। यदि AQ = 3.5cm, PC =4.5cm और BR = 7cm है, तो त्रिभुज ABC की परिधि (सेमी में) है:
View Solution