∫sinxlog(cosx)dx=?
A
cosxlog(cosx)−cosx+C
B
−cosxlog(cosx)+cosx+C
C
cosxlog(cosx)+cosx+C
D
none of these
Video Solution
Text Solution
The correct Answer is:B
Put cos x=t and - sin x dx=dt.
∴ I=−∫logtdt=−∫(logtI⋅1II)dt=−[(logt)t−∫1t⋅tdt]
=−t(logt)+t+C=−cost[log(cost)]+cosx+C.
|
Topper's Solved these Questions
Similar Questions
Evaluate the following integrals:
∫xexdx
View SolutionConstruct a 2×3 matrix whose elements are given by
aij=12(i−2j)2.
View SolutionLet S1 and S2 be the two switches and let their probabilities of working be given by P(S1)=⅘ and P(S2)=.9/10. Find the probability that the current flows from the terminal a to terminal A to terminal B when S1 and S2 are installed in series, shown as follows :
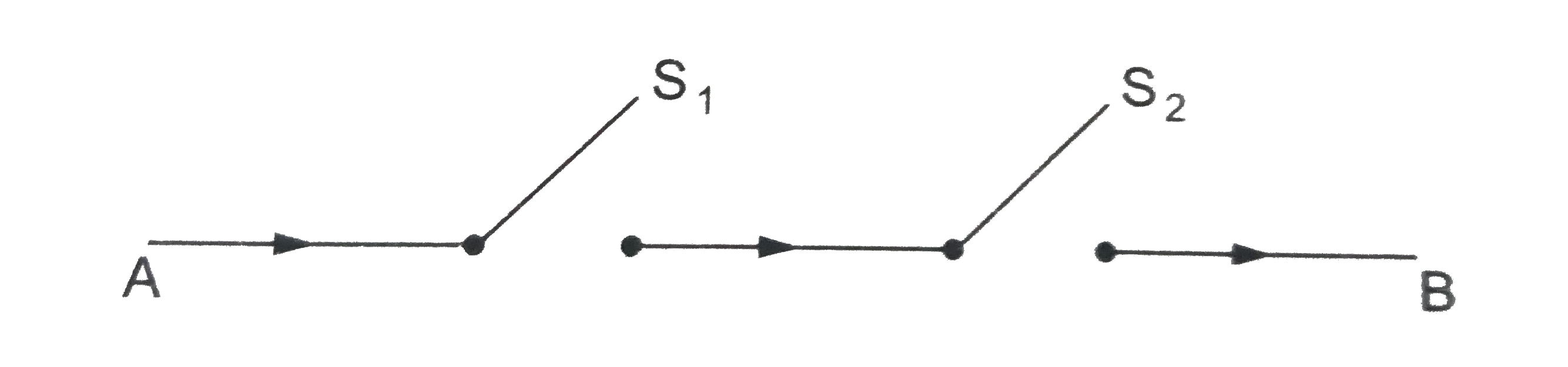
View Solution∫1−cosxcosx(1+cosx)dx
View Solution∫1−cosxcosx(1+cosx)dx
View Solution∫cosx(1+cosx)dx=?
View Solution∫cosx1+cosxdx
View Solution∫cosxsinx+cosxdx=
View Solution∫cosx1+cosxdx=
View Solution∫cosx1−cosxdx=
View Solution∫dxcosx(1−cosx)=
View Solution∫sinxlog(secx+tanx)dx=
View Solution∫1cosx(1+cosx)dx=
View Solution∫cosxcosx−sinxdx=
View Solution∫1−cosxcosx(1+cosx)dx
View Solution

