A steel uniform rod of length 2L cross sectional area A and mass Mis set rotating in a horizontal plane about an axis passing through the centre. If Y is the Young's modulus for steel, find the extension in the length of the rod.Solution in Gujrati
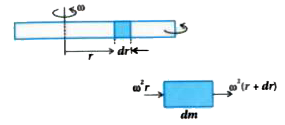
Let us consider an element of width dr at a distance r from the given axis of rotation as showin in the diagram.
Suppose tention in the rod at r and dr distance are T(r)andT(r+dr)
Centripetal force acting on small length element
F=dmrω2 [∵FC=mrω2]
∴F=μrω2dr ...(1)
[∵μ=dmdr⇒dm=μdr]
∴T(r)−T(r+dr)=μrω2dr
[∵T(r)−T(r+dr)= resultant force F]
∴−dT=μrω2dr
Centripetal force and tension force are opposite to each other hence negative sign present.
Integrating on both side.
∫T=0T=TdT=μω2∫lrrdr
−[T]0T=μω2[r22]lr
∴−[0−T]=μω22[l2−r2]
∴T=μω22(l2−r2) ...(2)
Now if Δr is the extension in the elemente of length dr
∴ Young.s modulus Y=T(r)A×drΔr
∴Δrdr=T(r)YA=TYA
∴Δrdr=μω22YA(l2−r2)
∴Δr=μω22YA∫(l2−r2)dr
Integrating on both side,
∫Δr=μω22YA∫(l2−r2)dr
∴Δr=μω22YA[l2r−r33]l0
∴Δr=μω22YA[[l3−l33]
∴Δr=μω22YA×2l33∴Δr=μω2l33YA
∴ Extension of Δr in both side length, then tota extension =2Δr
=2μω2l33YA
Similar Questions
A steel rod of length L_0 . has a cross sectional area A. The force required to stretch this rod by the same amount as the expansion produced by heating it through DeltaT is (coefficient of linear expansion of steel is alpha and young's modulus for steel is Y ).
View SolutionA stell rod of length 2l corss sectional area A and mass M is set rotating in a horizotnal plane about an axis passing through its cnetre and perpendicular to its length with constant angular velcoty ω. If Y is the Young's modulus for steel, find the extension in the lenght of the rod. (Assume the rod is uniform.)
View SolutionA uniform steel rod of length 1m and area of cross section 20cm2 is hanging from a fixed support. Find the increase in the length of the rod.
View SolutionA uniform rod of mass m. length L, area of cross- secticn A is rotated about an axis passing through one of its ends and perpendicular to its length with constant angular velocity \(omega\) in a horizontal plane If Y is the Young's modulus of the material of rod, the increase in its length due to rotation of rod is
View Solutionलंबाई 21, अनुप्रस्थ काट क्षेत्रफल Aतथा द्रव्यमान Mकी कोई स्टील की छड़ अपने केंद्र से गुजरने वाले अक्ष के परितः क्षेतिज तल में पूर्णन कराई जाती है। यदि स्टील का यंग गुणांक Y है, तो छड़ की लंबाई में वृद्धि ज्ञात कीजिए। (छड़ को एक समान मानिए )।
View SolutionA uniform rod of length l, mass m, cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity ω. Find the total extension in the rod due to the tension produced in the rod.
View SolutionA rod of length L kept on a smooth horizontal surface is pulled along its length by a force F. The area of cross-section is A and Young's modulus is Y. The extension in the rod is
View Solution

