Given P(x) =x4+ax3+bx2+cx+d such that x=0 is the only real root of P'(x) =0 . If P(-1) lt P(1),then∈the∫erval[-1,1]
P(−1) is the minimum but P(1) is not the maximum of P
neither P(−1) is the minimum nor P(1) is the maximum of P
P(−1) is the minimum and P(1) is the maximum of P
P(−1) is not minimum but P(1) is the maximum of P
The correct Answer is:D
Step by step video, text & image solution for Given P(x) =x^(4) +ax^(3) +bx^(2) +cx +d such that x=0 is the only real root of P'(x) =0 . If P(-1) lt P(1), then in the interval [-1,1] by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVESBook:MCGROW HILL PUBLICATIONChapter:APPLICATIONS OF DERIVATIVESExercise:Question for Previous Year.s B-Architecture Entrance Examination Papers
Explore 27 Videos
- APPLICATIONS OF DERIVATIVESBook:MCGROW HILL PUBLICATIONChapter:APPLICATIONS OF DERIVATIVESExercise:Exercise ( NUMERICAL ANSWER TYPE QUESTIONS)
Explore 17 Videos
- AREA BY INTEGRATIONBook:MCGROW HILL PUBLICATIONChapter:AREA BY INTEGRATIONExercise:Question from Previous Years. B-Architecture Entrance Examination Papers
Explore 12 Videos
Similar Questions
The slope of the normal to curve y=x3−4x2 at (2,−1) is
View SolutionIf the tangent at (16,64) on the curve y2=x3 meets the curve again at Q(u, v) then uv is equal to_____
View SolutionThe area enclosed by the parabola y=3(1−x2) and the x-axis is
View SolutionGiven P(x)=x4+ax3+cx+d such that x=0 is the only real root of P'(x)=0.IfP(1)<P(1) , then in the interval [1,1] . (1) P(1) is the minimum and P(1) is the maximum of P (2) P(1) is not minimum but P(1) is the maximum of P (3) P(1) is the minimum but P(1) is not the maximum of P (4) neither P(1) is the minimum nor P(1) is the maximum of P
View SolutionLet P(x)=x4+ax3+bx2+cx+d be a polynomial such that P(1)=1,P(2)=8,+P(3)=27,P(4)=64 then the value of 152−P(5) is____________.
View SolutionLet P(x)=x^(4)+ax^(3)+bx^(2)+cx+d be a polynomial such that P(1)=1,P(2)=8,P(3)=27,P(4)=64 then find P(10)
View SolutionGiven P(x) =x4+ax3+bx2+cx+d such that x=0 is the only real root of P'(x) =0 . If P(-1) < P(1), then in the interval [−1,1]
View SolutionIn the given figure graph of y=p(x)=x4+ax3+bx2+cx+d is given
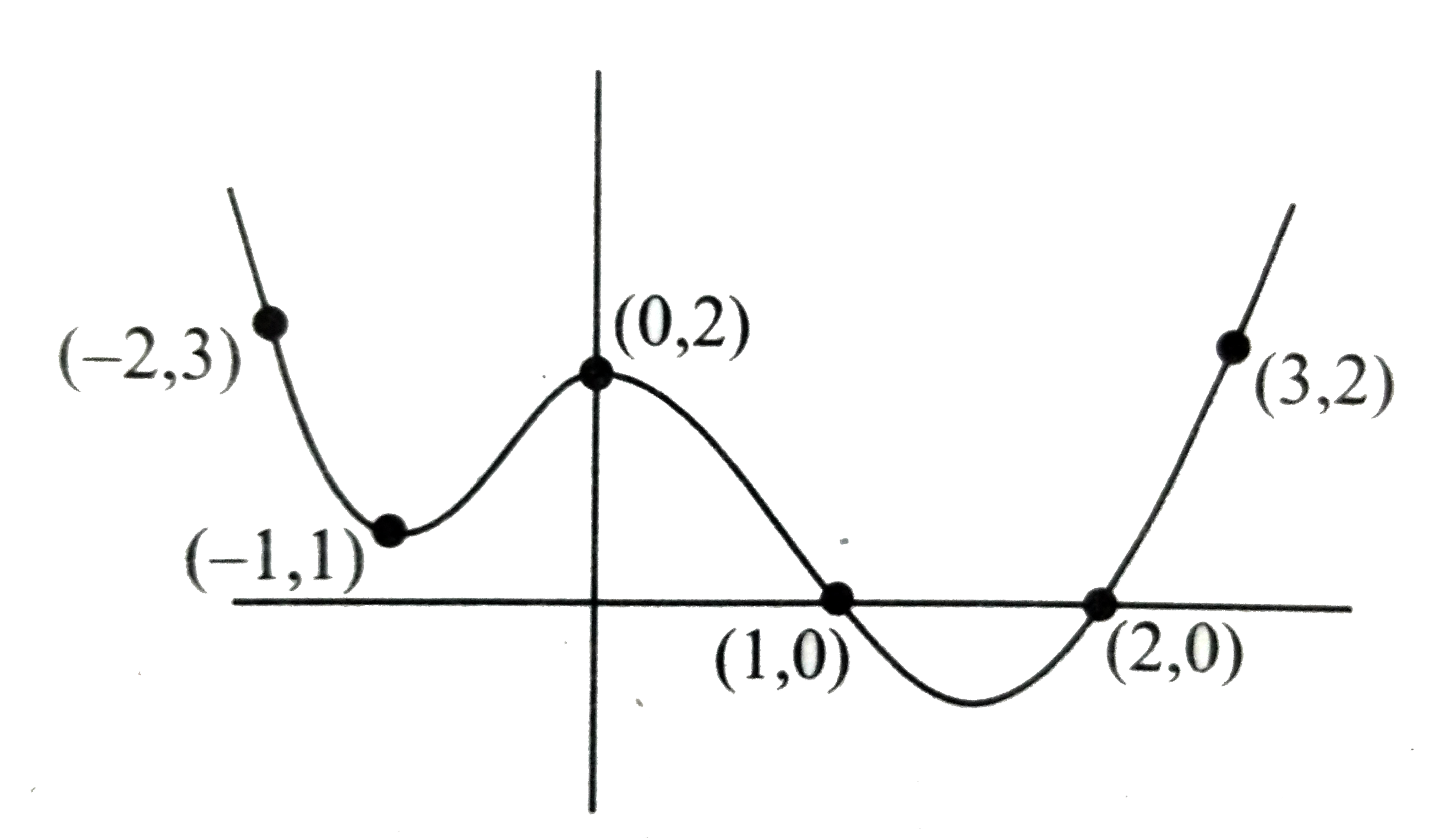
The product of all imaginery roots of p(x)=(0) is
View SolutionIf P(x)=x^(4)+ax^(3)+bx^(2)+cx+d,P(1)=P2=P(3)=0 then find P(4)
View SolutionGiven P(x)=x4+ax3+bx2+cx+d such that x=0 is the only real root of P'(x)==0. If P(−1)<P(1), then in the interval [-1,1]
View SolutionGiven P(x)=x^(4)+ax^(3)+ + bx^(2)+cx+d such that x =0 is the only real root of p'' (x)=0 . If P(-1) lt P(1) , then in the interval [-1, 1] :
View SolutionGiven P(x) =x^(4) +ax^(3) +bx^(2) +cx +d such that x=0 is the only real root of P'(x) =0 . If P(-1) lt P(1), then in the interval [-1,1]
View Solutionमाना P(x)=x4+ax3+bx2+cx+d के लिए x=0 ही अकेला P'(x)=0 का वास्तविक मूल है। यदि P(−1)<P(1) है , तब अंतराल [−1,1] में
View Solutionagreed P(x)=x^(4)+ax^(3)=bx^(2)+cx+d For x = 0 alone P'(x)=0 Is the real root of. If P(-1)ltP(1) Is then the interval [-1,1] in
View SolutionGiven P(x)=x^(4)+ax^(3)+bx^(2)+cx +d such that x=0 is the only real root of P'(x)==0 . If P(-1) lt P(1) , then in the interval [-1,1]
View SolutionGiven P(x)=x4+ax3+bx2+cx+d such that x=0 is the only real root of P'(x)==0. If P(−1)<P(1), then in the interval [-1,1]
View Solution
