Constant temperature of ends are T1 and T2 (where T1>T2) for a conducting rod of 'L' length and cross-sectional area A. What would be the rate of heat transfer in thermal steady state ? Solution in Gujrati
dQdt=KA(T1−T2)L
dQdt=KAL(T1−T2)
dQdt=KA(T1−T2)2
dQdt=KL(T1−T2)A
The correct Answer is:C
Knowledge based question
Similar Questions
An amount of heat passing through a metallic rod in time t is given by Q=(KA(T_(1)-T_(2))t)/(I) where k= thermal conductivity A= Cross sectional area, T_(1) and T_(2) are temeprature of hot and cold ends respectively and L= length. So the dimesional formula for k=.....
View SolutionA rod of length l and of a uniform cross-sectional area A is made of a material of non-uniform thermal conductivity. Its thermal conductivity is temperature depenndent and varies as K=(B)/(T) , where B is a constant. If ends of the rod are maintained at constant temperatures T_(1) and T_(2) with T_(1)gt T_(2) , rate of flow of heat in steady state will be :
View SolutionEleven rods each of length L , cross section A and coeffeicient of thermal conductivity K are arranged as shown . Find the rate of heat transfere from P to Q(T1>T2) .
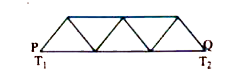
View SolutionThree rods of same cross-section but different length and conductivity are joined in series . If the temperature of the two extreme ends are T1andT2(T1>T2) find the rate of heat transfer H.

View Solutionएक छड जिसकी लम्बाई l और अनुप्रस्थ काट क्षेत्रफल A है की परिवर्ती ऊष्माचालकता k=αT, से दी जाती है, जहाँ α एक धनात्मक नियतांक है और T केल्विन में तापमान है छड़ के दोनों किनारे ताप T1 और T2(T1>T2) पर बने रहते हैं। छड़ से प्रवाहित ऊष्मीय धारा होगी-
View SolutionThe two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperature T_(1) and T_(2) (T_(1) gt T_(2)) . The rate of heat transfer. (dQ)/(dt) , through the rod in a steady state is given by
View SolutionOne end of a rod of length L and crosssectional area A is kept in a furnace at temperature T1. The other end of the rod is kept at a temperature T2. The thermal conductivity of the matrieal of the rod is K and emissivity of the rod is e. It is gives that T!=Ts+ΔT, where ΔT<<Ts,Ts is the temperature of the surroundings. If ΔT∝(T1−T2) find the proportional constant, consider that heat is lost only by rediation at the end where the temperature of the rod is T1.

View SolutionA rod of length l and cross-section area A has a variable thermal conductivity given by K = alpha T, where alpha is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T_(1) and T_(2) (T_(1)gtT_(2)) . Heat current flowing through the rod will be
View Solution
