A simple pendulum has a length L and a bob of mass m. The bob is oscillating with amplitude A. Show that the maximum tension (T) in the string is (for small angular displacement).
Tmax=mg[1+(AL)2].Solution in Gujrati
Here, Mass of bob =m, Amplitude of oscillation = A, Length of pendulum = L, ∠BAC=θ
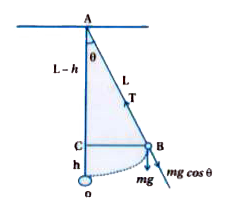
Tension T=mgcosθ+mv2L [mv2L= centripetal force ]
If cosθ=1
v=vmax and T=Tmax
Tmax=mg+mv2maxL ...........(1)
=mg+mA2ω2L but ω2=gL
Tmax=mg+mA2gL×L ..........(2)
∴Tmax=mg+mgA2L2
∴Tmax=mg[1+(AL)2].
Similar Questions
A simple pendulum of length .l. carries a bob of mass m. If the breaking strenght of the string is 2 mg, the maximum angular amplitude from the vertical can be
View SolutionA simple pendulum with length L and mass m of the bob is vibrating with an amplitude a. then the maximum tension in the string is not:
View SolutionA simple pendulum of length L having bob of mass M is vibrating with amplitude a. Then the maximum tension in the string is
View SolutionA simple pendulum of length .l. carries a bob of mass m. If the breaking strenght of the string is 2 mg, the maximum angular amplitude from the vertical can be
View SolutionA simple pendulum of length l having bob of mass M is vibrating with amplitude a. Then the maximum tension in the string is
View SolutionA simple pendulum of length l having bob of mass M is vibrating with amplitude a. Then the maximum tension in the string is
View SolutionA simple pendulum of length l has a maximum angular displacement θ. The maximum kinetic energy of the bob of mass m will be
View SolutionA simple pendulum of length l has maximum angular displacement θ . Then maximum kinetic energy of a bob of mass m is
View Solution

