On screen there are two bright points at a distance I mm. These points are observed by the person whose eye is having diameter 3 mm from which maximum distance this person can observe them resolved ?Solution in Gujrati
6 m
3 m
5 m
1 m
The correct Answer is:C

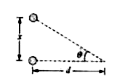
Resolution power =1.22λd
and sinθ≈=yD
∴yD=1.22λd
∴D=yd1.22λ=10−3×3×10−31.22×5×10−7=306.1=5m
Similar Questions
Distance between two points on paper is They are observed such that view line observer is perpendicular to them. Diameter lens of an eye of an observer is 2 mm. Fo which minimum value of d both points will h observed ?
View SolutionInterference fringes are observed on a screen by illuminating two thin slits 1 mm apart with a light source (lambda=632.8 nm) . The distance between the screen and the slits is 100 cm. If a bright fringes is observed on a screen at a distance of 1.27 mm from the central bright fringe , then the path difference between the waves , which are reaching this point from the slits is close to :
View SolutionTwo point white dots are 1 mm apart on a black paper. They are viewed by eye of pupil diameter 3 mm. Approximately, what is the maximum distance at which these dots can be resolved by the eye ? [Take wavelength of light = 500 nm]
View Solutionएक काले कागज पर दो सफेद बिंदु 1 mm दूरी पर हैं। उन्हें 3 mm व्यास की पुतली के एक नेत्र द्वारा देखा जाता है। वह अधिकतम दूरी लगभग क्या है जिस पर इन बिंदुओं को नेत्र द्वारा विभेदित किया जा सकता है? [प्रकाश की तरंग दैर्ध्य = 500 nm लीजिए]
View SolutionThe defect of eye in which the far point of persons will be at a definite distance from eye is.............
View SolutionTwo point white dots are 1 mm apart on a black paper. They are viewed by eye of pupil diameter 3 mm. Approximately, what is the maximum distance at which dots can be resolved by the eye? [Take wavelength of light = 500 nm]
View SolutionTwo point white dots are 1 mm apart on a black paper. They are viewed by eye of pupil diameter 3 mm. Approximately, what is the maximum distance at which these dots can be resolved by the eye? [Take wavelength of light=500 nm)
View Solution
