A mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the Uv to the red end of the visible spectrum. In our experiment with rubidium photo-cell, the following lines from a mercury source were used:
λ1=3650Å,λ2=4047Å,λ3=4358Å,λ4=5461Å,λ5=6907Å,
The stopping voltages, respectively, were measured to be:
V01=1.28V,V02=0.95V,V03=0.74V,V04=0.16V,V05=0V
Determine the value of Planck’s constant h, the threshold frequency and work function for the material.
[Note: You will notice that to get h from the data, you will need to know e (which you can take to be 1.6×10−19C). Experiments of this kind on Na, Li, K, etc. were performed by Millikan, who, using his own value of e (from the oil-drop experiment) confirmed Einstein’s photoelectric equation and at the same time gave an independent estimate of the value of h.]Solution in Gujrati
(a)From frequency v=cλ,
V1=cλ1=3×1083650×10−10=8.219×1014Hz
V2=cλ2=3×1084047×10−10=7.412×1014Hz
V3=cλ3=3×1084358×10−10=6.884×1014Hz
V4=cλ4=3×1085461×1010=5.493×1014Hz
V5=cλ5=3×1086907×10−10=4.343×1014Hz
∴
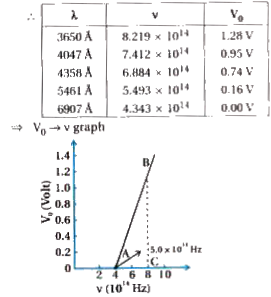
Slope of graph=BCAC
ΔV0ΔV=1.28−0(8.2−5.0)×1014
=1.28302×1014=0.4×10−14
=4×10−15Vs
⇒From Einstein.s photoelectric equation,
eV0=hV−ϕ0
∴eΔV0=hΔV[∵ϕ0=constant]
∴ΔV0ΔV=he
∴h=e×ΔV0Δv
=1.6×10−19×4.0×10−15
=6.4×10−34Js
(b)Threshold frequency,
V0=5.0×1014Hz
Which is obtained from V0→v graph.
Work function.
ϕ0=hv0
=6.63×10−34×5×1014
=33.15×10−20J =33.15×10−201.6×10−19
Similar Questions
A mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the Uv to the red end of the visible spectrum. In our experiment with rubidium photo-cell, the following lines from a mercury source were used: lambda_(1) = 3650 Å, lambda_(2) = 4047 Å, lambda_(3) = 4358 Å, lambda_(4) = 5461 Å, lambda_(5) = 6907 Å , The stopping voltages, respectively, were measured to be: V_(01) = 1.28 V, V_(02) = 0.95 V, V_(03) = 0.74 V, V_(04) = 0.16 V, V_(05) = 0 V Determine the value of Planck’s constant h, the threshold frequency and work function for the material. [Note: You will notice that to get h from the data, you will need to know e (which you can take to be 1.6 xx 10^(-19) C ). Experiments of this kind on Na, Li, K, etc. were performed by Millikan, who, using his own value of e (from the oil-drop experiment) confirmed Einstein’s photoelectric equation and at the same time gave an independent estimate of the value of h.]
View Solutionएक पारद लैंप, प्रकाश विद्युत उत्सर्जन की आवृत्ति निर्भरता के अध्ययन के लिए एक सुविधाजनक स्त्रोत है क्योंकि यह दृश्य –स्पेक्ट्रम के परबैंगनी (UV) के लाल छोर तक कइ वर्ण रेखाएं उत्सर्जित करता हैं रूबीडियम प्रकाश सेल के हमारे प्रयोग में पारद स्त्रोत की निम्न वर्ण रेखाओं का प्रयोग किया गया
λ1=3650Å,λ2=4047Å,λ3=4358Å,λ4=5461Å,λ5=6907Å,
निरोधी वोल्टताएं क्रमशः निम्न मापी गई
V01=1.28V,V02=0.95V,V03=0.74V,V04=0.16V,V05=0V
(a) प्लैंक स्थिरांक h का मान ज्ञात कीजिए।
(b) धातु के लिए देहली आवृत्ति तथा कार्य फलन का आकलन कीजिए।
View SolutionA mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the Uv to the red end of the visible spectrum. In our experiment with rubidium photo-cell, the following lines from a mercury source were used: lambda_(1) = 3650 Å, lambda_(2) = 4047 Å, lambda_(3) = 4358 Å, lambda_(4) = 5461 Å, lambda_(5) = 6907 Å , The stopping voltages, respectively, were measured to be: V_(01) = 1.28 V, V_(02) = 0.95 V, V_(03) = 0.74 V, V_(04) = 0.16 V, V_(05) = 0 V Determine the value of Planck’s constant h, the threshold frequency and work function for the material. [Note: You will notice that to get h from the data, you will need to know e (which you can take to be 1.6 xx 10^(-19) C ). Experiments of this kind on Na, Li, K, etc. were performed by Millikan, who, using his own value of e (from the oil-drop experiment) confirmed Einstein’s photoelectric equation and at the same time gave an independent estimate of the value of h.]
View SolutionLights of wavelengths λ1=4500Å,λ2=6000Å are sent through a double slit arrangement simultaneously. Then
View SolutionA mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the end of the red visible spectrum. In our experiment with rubidium photocell, the following lines from a mercury source were used: λ1=3650A∘,λ2=4047A∘,λ3=4358A∘,λ4=5461A∘,λ5=6907A∘ The stopping voltages, respectively were measured to be:
V01=1.28V,V02=0.95V,V03=0.74V,V04=0.16V,V05=0V.
(a) Determine the value of Planck's constant h.
(b) Estimate the threshold frequency and work function for the material.
View SolutionLast line of bracket series for H-atom has wavelength lambda_(1)"Å" and 2nd line of Lyman series has wavelength lambda_(2)"Å" then:
View SolutionA mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the red end of the visible spectrum. In our experiment with rubidium photocell, the following lines from a mercury source were used:
λ1=3650Å,λ2=4047Å,λ3=4358Å,λ4=5461Å,λ5=6907Å
The stopping voltages respectively were measured to be
V01=1.28V,V02=0.95V,V03=0.74V,V04=0.16V,V05=0
Determine the value of Planck.s constant h, the threshold frequency and work function for the material.
View SolutionThe ratio of resolving powers of an optical microscope for two wavelengths lambda_(1) = 4000 Å and lambda_(2) = 6000 Å is
View Solution
